题目内容
设a为实数,记函数 的最大值为
的最大值为 .
.
(1)设t= ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ;
(2)求 ;
;
(3)试求满足 的所有实数a.
的所有实数a.
 的最大值为
的最大值为 .
.(1)设t=
 ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ;(2)求
 ;
;(3)试求满足
 的所有实数a.
的所有实数a.(1)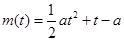 ,
,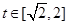 ;(2)
;(2) =
=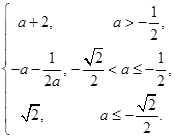 (3)
(3)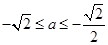 .
.
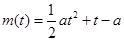 ,
,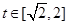 ;(2)
;(2) =
=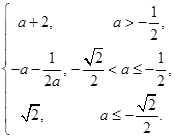 (3)
(3)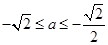 .
.试题分析:(1)根据
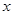 的取值范围求出
的取值范围求出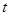 的范围,再将
的范围,再将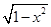 用含
用含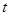 的式子表示;(2)由题意知
的式子表示;(2)由题意知 即为函数
即为函数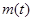
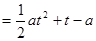 ,
,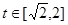 的最大值,因为对称轴含有参数
的最大值,因为对称轴含有参数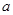 ,所以要讨论处理;(3)根据(2)问得出的
,所以要讨论处理;(3)根据(2)问得出的 ,由
,由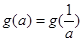 在对应区域上讨论解答即可.
在对应区域上讨论解答即可.试题解析:(1)∵
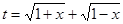 ,∴要使
,∴要使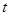 有意义,必须
有意义,必须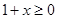 且
且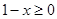 ,即
,即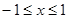 .
.∵
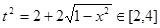 ,且
,且 ①
① ∴
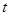 的取值范围是
的取值范围是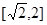 , 2分
, 2分由①得:
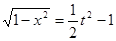 ,
,∴
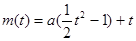
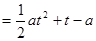 ,
,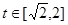 . 4分
. 4分(2)由题意知
 即为函数
即为函数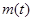
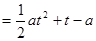 ,
,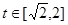 的最大值,
的最大值,∵直线
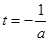 是抛物线
是抛物线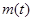
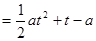 的对称轴, 5分
的对称轴, 5分∴可分以下几种情况进行讨论:
①当
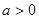 时,函数
时,函数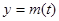 ,
,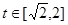 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,由
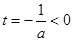 知
知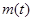 在
在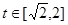 上单调递增,故
上单调递增,故
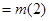
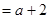 ;
;②当
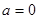 时,
时,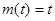 ,
,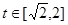 ,有
,有 =2;
=2;③当
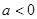 时,,函数
时,,函数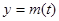 ,
,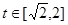 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,若
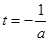
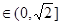 即
即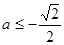 时,
时,
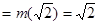 ,
,若
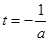
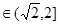 即
即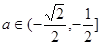 时,
时,
 ,
,若
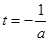
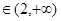 即
即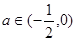 时,
时,
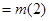
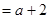 . 9分
. 9分综上所述,有
 =
=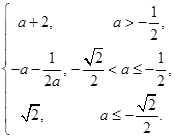 10分
10分(3)当
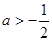 时,
时,
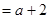
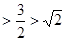 ;
;当
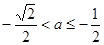 时,
时,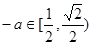 ,
,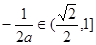 ,∴
,∴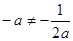 ,
,
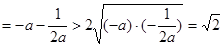 ,故当
,故当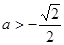 时,
时,
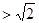 ;
; 当
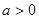 时,
时,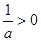 ,由
,由
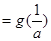 知:
知: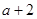
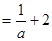 ,故
,故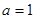 ;
;当
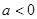 时,
时,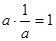 ,故
,故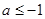 或
或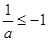 ,从而有
,从而有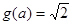 或
或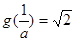 ,
,要使

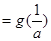 ,必须有
,必须有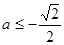 ,
,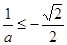 ,即
,即 ,
,此时,
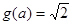
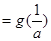 . 13分
. 13分 
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
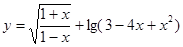 的定义域为
的定义域为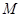 ,
,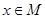 时,求
时,求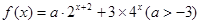 的最小值.
的最小值.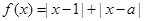 .
.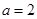 ,解不等式
,解不等式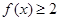 ;
;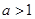 ,
,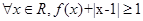 ,求实数
,求实数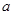 的取值范围.
的取值范围.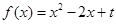 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.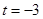 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;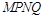 的面积的最大值。
的面积的最大值。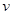 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度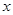 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当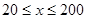 时,车流速度
时,车流速度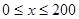 时,求函数
时,求函数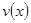 的表达式;
的表达式;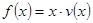 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时). ,其中
,其中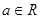 ,若对任意的非零实数
,若对任意的非零实数 ,存在唯一的非零实数
,存在唯一的非零实数 ,使得
,使得 成立,则k的最小值为( )
成立,则k的最小值为( )
 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )



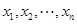 中的最大数为max{
中的最大数为max{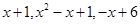 }}= ( )
}}= ( )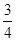
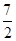
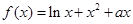 .
.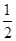 时,
时,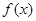 取得极值,求
取得极值,求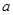 的值;
的值;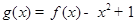 ,当
,当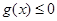 在其定义域内恒成立,并证明
在其定义域内恒成立,并证明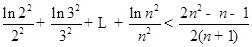 (
(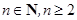 ).
).