题目内容
已知集合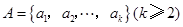 ,其中
,其中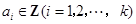 ,由
,由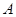 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: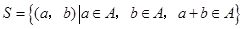 ,
,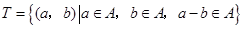 .其中
.其中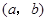 是有序数对,集合
是有序数对,集合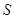 和
和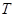 中的元素个数分别为
中的元素个数分别为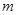 和
和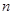 .若对于任意的
.若对于任意的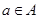 ,总有
,总有 ,则称集合
,则称集合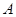 具有性质
具有性质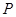 .
.
(I)检验集合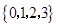 与
与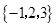 是否具有性质
是否具有性质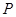 并对其中具有性质
并对其中具有性质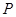 的集合,写出相应的集合
的集合,写出相应的集合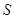 和
和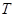 ;
;
(II)对任何具有性质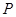 的集合
的集合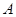 ,证明:
,证明: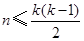 ;
;
(III)判断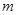 和
和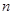 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
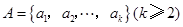 ,其中
,其中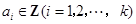 ,由
,由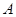 中的元素构成两个相应的集合:
中的元素构成两个相应的集合: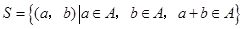 ,
,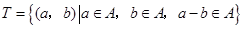 .其中
.其中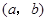 是有序数对,集合
是有序数对,集合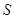 和
和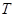 中的元素个数分别为
中的元素个数分别为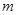 和
和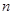 .若对于任意的
.若对于任意的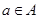 ,总有
,总有 ,则称集合
,则称集合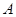 具有性质
具有性质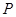 .
.(I)检验集合
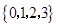 与
与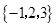 是否具有性质
是否具有性质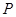 并对其中具有性质
并对其中具有性质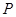 的集合,写出相应的集合
的集合,写出相应的集合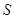 和
和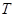 ;
;(II)对任何具有性质
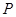 的集合
的集合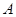 ,证明:
,证明: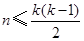 ;
;(III)判断
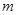 和
和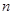 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.(I)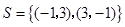 ;
;
(II)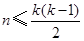
(III)
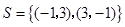 ;
;
(II)
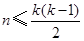
(III)

解:集合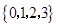 不具有性质
不具有性质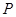 .
.
集合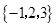 具有性质
具有性质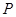 ,其相应的集合
,其相应的集合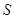 和
和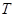 是
是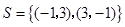 ,
,
 .
.
(II)证明:首先,由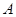 中元素构成的有序数对
中元素构成的有序数对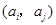 共有
共有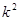 个.
个.
因为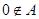 ,所以
,所以 ;
;
又因为当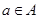 时,
时, 时,
时, ,所以当
,所以当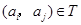 时,
时,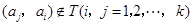 .
.
从而,集合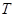 中元素的个数最多为
中元素的个数最多为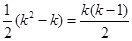 ,
,
即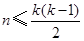 .
.
(III)解: ,证明如下:
,证明如下:
(1)对于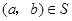 ,根据定义,
,根据定义,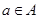 ,
,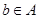 ,且
,且 ,从而
,从而 .
.
如果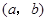 与
与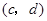 是
是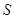 的不同元素,那么
的不同元素,那么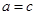 与
与 中至少有一个不成立,从而
中至少有一个不成立,从而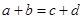 与
与 中也至少有一个不成立.
中也至少有一个不成立.
故 与
与 也是
也是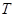 的不同元素.
的不同元素.
可见,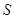 中元素的个数不多于
中元素的个数不多于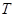 中元素的个数,即
中元素的个数,即 ,
,
(2)对于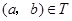 ,根据定义,
,根据定义,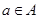 ,
,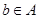 ,且
,且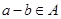 ,从而
,从而 .如果
.如果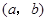 与
与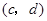 是
是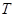 的不同元素,那么
的不同元素,那么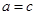 与
与 中至少有一个不成立,从而
中至少有一个不成立,从而 与
与 中也不至少有一个不成立,
中也不至少有一个不成立,
故 与
与 也是
也是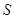 的不同元素.
的不同元素.
可见,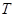 中元素的个数不多于
中元素的个数不多于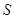 中元素的个数,即
中元素的个数,即 ,
,
由(1)(2)可知, .
.
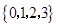 不具有性质
不具有性质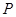 .
.集合
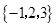 具有性质
具有性质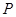 ,其相应的集合
,其相应的集合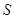 和
和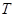 是
是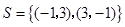 ,
, .
.(II)证明:首先,由
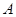 中元素构成的有序数对
中元素构成的有序数对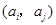 共有
共有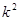 个.
个.因为
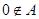 ,所以
,所以 ;
;又因为当
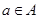 时,
时, 时,
时, ,所以当
,所以当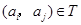 时,
时,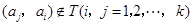 .
.从而,集合
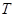 中元素的个数最多为
中元素的个数最多为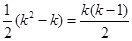 ,
,即
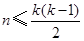 .
.(III)解:
 ,证明如下:
,证明如下:(1)对于
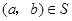 ,根据定义,
,根据定义,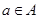 ,
,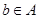 ,且
,且 ,从而
,从而 .
.如果
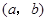 与
与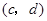 是
是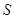 的不同元素,那么
的不同元素,那么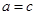 与
与 中至少有一个不成立,从而
中至少有一个不成立,从而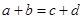 与
与 中也至少有一个不成立.
中也至少有一个不成立.故
 与
与 也是
也是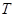 的不同元素.
的不同元素.可见,
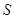 中元素的个数不多于
中元素的个数不多于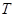 中元素的个数,即
中元素的个数,即 ,
,(2)对于
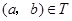 ,根据定义,
,根据定义,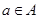 ,
,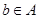 ,且
,且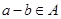 ,从而
,从而 .如果
.如果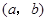 与
与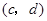 是
是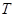 的不同元素,那么
的不同元素,那么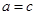 与
与 中至少有一个不成立,从而
中至少有一个不成立,从而 与
与 中也不至少有一个不成立,
中也不至少有一个不成立,故
 与
与 也是
也是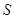 的不同元素.
的不同元素.可见,
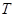 中元素的个数不多于
中元素的个数不多于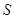 中元素的个数,即
中元素的个数,即 ,
,由(1)(2)可知,
 .
.
练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目



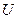 是实数集
是实数集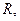
 ,
,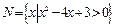
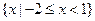
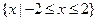
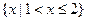
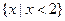
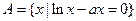 恰有三个真子集,则
恰有三个真子集,则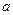 的取值范围为 ▲ .
的取值范围为 ▲ .  ,集合
,集合 ,则集合
,则集合 有几个元素( )
有几个元素( )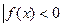 } N={x
} N={x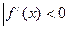 },若M
},若M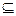 N,则实数a的取值范围是 。
N,则实数a的取值范围是 。 ,集合
,集合 ,则
,则 ;
;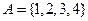 ,那么
,那么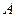 的真子集的个数是( )
的真子集的个数是( )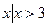 },B={
},B={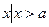 },且A
},且A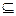 B,则a的取值范围为 .
B,则a的取值范围为 .