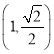题目内容
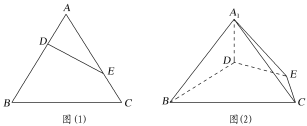
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(Ⅱ)设![]() .若
.若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)极小值0,无极大值;(Ⅱ)![]() .
.
【解析】
(Ⅰ)![]() ,令
,令![]() ,
,![]() 得到
得到![]() 的单调性即可得到极值;
的单调性即可得到极值;
(Ⅱ)![]() 在
在![]() 上恒成立,可构造函数
上恒成立,可构造函数![]() ,
,![]() ,令
,令![]() ,
,![]() ,分
,分![]() ,
,![]() ,
,![]() 讨论即可.
讨论即可.
![]() 当
当![]() 时,
时,![]()
则![]() ,
,![]()
令![]()
解得![]() (舍去),
(舍去),![]() .
.
当![]() 时,
时,![]()
![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]()
![]() 在
在![]() 上单调递增,
上单调递增,![]() 的极小值为
的极小值为![]() ,无极大值.
,无极大值.
![]()
![]()
若![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
构造函数![]() ,
,
则![]()
令![]() .
.
![]()
![]() 若
若![]() 可知
可知![]() 恒成立.
恒成立.
![]() 在
在![]() 上单调递增.
上单调递增.
![]() .
.
![]() 当
当![]() 即
即![]() 时,
时,
![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
![]() 在
在![]() 上恒成立,
上恒成立,![]() 满足条件.
满足条件.
![]() 当
当![]() 即
即![]() 时,
时,
![]() ,
,
![]() 存在唯一的
存在唯一的![]() 使得
使得![]() .
.
当![]() 时,
时,![]() 即
即![]()
![]() 在
在![]() 单调递减.
单调递减.
![]() ,这与
,这与![]() 矛盾.
矛盾.
![]() 若
若![]() 由
由![]()
可得![]() (舍去),
(舍去),![]()
易知![]() 在
在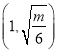 上单调递减.
上单调递减.
![]() 在
在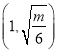 上恒成立,
上恒成立,
即![]() 在
在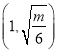 上恒成立.
上恒成立.
![]() 在
在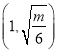 上单调递减.
上单调递减.
![]() 在
在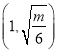 上恒成立,这与
上恒成立,这与![]() 矛盾.
矛盾.
综上,实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评,同时也为公司赢得丰厚的利润.该公司![]() 年至
年至![]() 年的年利润
年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关).
的统计数据如下表(已知该公司的年利润与年份代号线性相关).
年份 |
|
|
|
|
|
|
|
年份代号 |
|
|
|
|
|
|
|
年利润 |
|
|
|
|
|
|
|
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 年(年份代号记为
年(年份代号记为![]() )的年利润;
)的年利润;
(Ⅱ)当统计表中某年年利润的实际值大于由(Ⅰ)中线性回归方程计算出该年利润的估计值时,称该年为![]() 级利润年,否则称为
级利润年,否则称为![]() 级利润年.将(Ⅰ)中预测的该公司
级利润年.将(Ⅰ)中预测的该公司![]() 年的年利润视作该年利润的实际值,现从
年的年利润视作该年利润的实际值,现从![]() 年至
年至![]() 年这
年这![]() 年中随机抽取
年中随机抽取![]() 年,求恰有
年,求恰有![]() 年为
年为![]() 级利润年的概率.
级利润年的概率.
参考公式: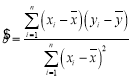 ,
,![]() .
.
【题目】凤梨穗龙眼原产厦门,是厦门市的名果,栽培历史已有100多年.龙眼干的级别按直径![]() 的大小分为四个等级(如下表).
的大小分为四个等级(如下表).
|
|
|
|
|
级别 | 三级品 | 二级品 | 一级品 | 特级品 |
某商家为了解某农场一批龙眼干的质量情况,随机抽取了100个龙眼干作为样本(直径分布在区间![]() ),统计得到这些龙眼干的直径的频数分布表如下:
),统计得到这些龙眼干的直径的频数分布表如下:
|
|
|
|
|
|
频数 | 1 |
| 29 |
| 7 |
用分层抽样的方法从样本的一级品和特级品中抽取6个,其中一级品有2个.
(1)求![]() 、
、![]() 的值,并估计这批龙眼干中特级品的比例;
的值,并估计这批龙眼干中特级品的比例;
(2)已知样本中的100个龙眼干约500克,该农场有500千克龙眼干待出售,商家提出两种收购方案:
方案![]() :以60元/千克收购;
:以60元/千克收购;
方案![]() :以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
:以级别分装收购,每袋100个,特级品40元/袋、一级品30元/袋、二级品20元/袋、三级品10元/袋.
用样本的频率分布估计总体分布,哪个方案农场的收益更高?并说明理由.