题目内容
2.若函数y=f(x)的定义域为[-3,2],则函数y=f(3-2x)的定义域是[$\frac{1}{2}$,3].分析 函数y=f(x)的定义域为[-3,2],直接由-3≤3-2x≤2求得x的范围得答案.
解答 解:∵函数y=f(x)的定义域为[-3,2],
∴由-3≤3-2x≤2,解得$\frac{1}{2}≤x≤3$.
故函数y=f(3-2x)的定义域是:[$\frac{1}{2}$,3].
故答案为:[$\frac{1}{2}$,3].
点评 本题考查函数的定义域及其求法,关键是掌握该类问题的解决方法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知f(x)=$\frac{a{x}^{2}-1}{x}$,且f′(x)≥0在定义域内恒成立,则a的取值范围为( )
| A. | [0,+∞) | B. | [0,1] | C. | [1,+∞) | D. | [-1,0] |
17.设a=log43,b=30.4,c=log3$\frac{1}{4}$,则( )
| A. | b>a>c | B. | a>c>b | C. | c>a>b | D. | a>b>c |
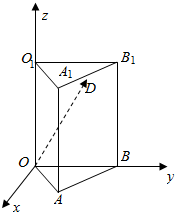 如图,在底面是边长为4的等边三角形的直三棱柱ABO-A1B1O1中,|AA1|=6,D为A1B1的中点,
如图,在底面是边长为4的等边三角形的直三棱柱ABO-A1B1O1中,|AA1|=6,D为A1B1的中点,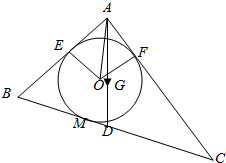 △ABC中,$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}$=$\overrightarrow{0}$O为△ABC内切圆的圆心,且AB=2,AC=3,BC=4.
△ABC中,$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}$=$\overrightarrow{0}$O为△ABC内切圆的圆心,且AB=2,AC=3,BC=4.