题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 是棱
是棱![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() 是棱
是棱![]() 的中点,求三棱锥
的中点,求三棱锥![]() 的体积与三棱柱
的体积与三棱柱![]() 的体积之比.
的体积之比.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AC1交A1C于点O,连接OD,由中位线定理可得OD∥BC1,故而BC1∥平面A1CD;(2)根据棱锥和棱柱的体积公式即可得出结论.
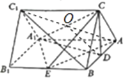
(1)证明:连接AC1交A1C于点O,连接OD,
∵CC1∥AA1,CC1=AA1,
∴四边形AA1C1C是平行四边形,
∴O是AC1的中点,又D是AB的中点,
∴OD∥BC1,又OD平面A1CD,BC1平面A1CD,
∴BC1∥平面A1CD.
(2)设三棱柱A1B1C1﹣ABC的高为h,则三棱柱A1B1C1﹣ABC的体积V=S△ABCh,
又V=V![]() V
V![]() ,V
,V![]() V
V![]() S△ABCh
S△ABCh![]() ,
,
∴V![]() ,
,
∵CC1∥BB1,CC1平面ABB1A1,BB1平面ABB1A1,
∴CC1∥平面ABB1A1,
∴V![]() V
V![]() ,
,
∵S![]() S
S![]() ,∴V
,∴V![]() V
V![]() ,
,
∴三棱锥C﹣AA1E的体积与三棱柱A1B1C1﹣ABC的体积之比为![]() .
.

练习册系列答案
相关题目





