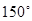题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,向量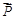 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
= (Ⅰ)求角B的大小;(Ⅱ)设
(Ⅰ)求角B的大小;(Ⅱ)设 =(sin(C+
=(sin(C+ ),
), ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值.
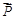 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
= (Ⅰ)求角B的大小;(Ⅱ)设
(Ⅰ)求角B的大小;(Ⅱ)设 =(sin(C+
=(sin(C+ ),
), ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值.(Ⅰ)B= .(Ⅱ)k=
.(Ⅱ)k=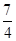 .
.
 .(Ⅱ)k=
.(Ⅱ)k=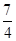 .
.试题分析:(Ⅰ)由条件
 =
= |,两边平方得
|,两边平方得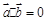 ,……2分
,……2分得(a-c)sinA+(b+c)(sinC-sinB)=0,
根据正弦定理,可化为a(a-c)+(b+c)(c-b)=0,即
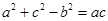 ,……4分
,……4分又由余弦定理
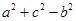 =2 a cosB,所以cosB=
=2 a cosB,所以cosB= ,B=
,B= .……6分
.……6分(Ⅱ)
 =(sin(C+
=(sin(C+ ),
), ),
), =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1), =2ksin(C+
=2ksin(C+ )+
)+ cos2A=2ksin(C+B)+
cos2A=2ksin(C+B)+ cos2A=2ksinA+
cos2A=2ksinA+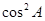 -
-
=-
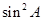 +2ksinA+
+2ksinA+ =-
=- +
+ (k>1).……8分
(k>1).……8分而0<A<
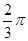 ,sinA∈(0,1],故当sinA=1时,
,sinA∈(0,1],故当sinA=1时, 取最大值为2k-
取最大值为2k- =3,得k=
=3,得k=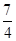 .……12分
.……12分点评:此类问题综合性强,要求学生熟练掌握有关正余弦定理及其变形的运用外,还要灵活运用三角函数的性质求最值

练习册系列答案
相关题目
 中,角
中,角 的对边分别为
的对边分别为 ,已知
,已知
 ;
; ,求
,求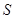 的最大值.
的最大值.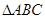 中,角
中,角 所对的边分别为
所对的边分别为 ,
, ,向量
,向量 ,且
,且

 。
。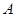 ;
;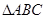 中,内角
中,内角 所对边分别是
所对边分别是 ,已知
,已知 ,
, ,则
,则 的三个内角
的三个内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 .
. 的值;
的值; ,求
,求 中,三个内角
中,三个内角 所对的边分别是
所对的边分别是 已知
已知 的面积等于
的面积等于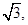 则
则
 中,边
中,边 所对的角分别为
所对的角分别为 ,
, ,则
,则 ( )
( )



 ,则角B的值为____________
,则角B的值为____________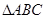 中,如果
中,如果 ,那么角
,那么角 等于 ( )
等于 ( )