题目内容
【题目】设动点![]() 是圆
是圆![]() 上任意一点,过
上任意一点,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,若点
,若点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 坐标为
坐标为![]() ,若直线
,若直线![]() ,
, ![]() 的斜率之和为定值3,求证:直线
的斜率之和为定值3,求证:直线![]() 必经过定点,并求出该定点的坐标.
必经过定点,并求出该定点的坐标.
【答案】(1)![]() .(2)见解析.
.(2)见解析.
【解析】试题分析:(1)设P、M的坐标,根据条件得两点坐标关系,再代入点![]() 满足的方程,化简得点
满足的方程,化简得点![]() 的轨迹的方程;(2)由题意
的轨迹的方程;(2)由题意![]() ,得
,得![]() .即得
.即得![]() ,再将直线方程代入椭圆方程,利用韦达定理化简得
,再将直线方程代入椭圆方程,利用韦达定理化简得![]()
最后根据点斜式特点得定点.
试题解析: 1)设点P、M的坐标分别为 (x,y)、 (x0,y0),由![]() ,得
,得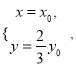
∴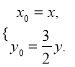
由点M在圆![]() 上,故
上,故![]() ,代入得
,代入得![]() .
.
∴ 点P的轨迹C的方程为 ![]() .
.
(2)当直线l的斜率不存在时,设直线l的方程为: ![]() ,
,
设A,B两点的坐标分别为 (x0,y0)、(x0, ![]() y0),
y0),
由题意![]() ,得
,得![]() ,解得
,解得![]() ,
,
所以直线l的方程为: ![]() .当直线l的斜率存在时,
.当直线l的斜率存在时,
设直线l的方程为y=kx+b,与C联立,
消元得![]() .
.
设A,B两点的坐标分别为 (x1,y1)、 (x2,y2),
则![]() ,
, ![]() (*).
(*).
由题意![]() ,得
,得![]() .
.
将y1=kx1+b和y2=kx2+b代入上式,可得![]() ,
,
所以![]() .(**)
.(**)
将(*)代入(**),化简得![]() ,解得
,解得![]() ,
,
代入直线l方程,得![]() .
.
不论b怎么变化,当![]() =0即x=
=0即x=![]() 时,
时, ![]() .
.
综上所述,直线l恒过定点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目