题目内容
15.△ABC的三边分别为a,b,c,边BC,CA,AB上的中线分别记ma,mb,mc,应用余弦定理证明:ma=$\frac{1}{2}$$\sqrt{2({b}^{2}+{c}^{2})-{a}^{2}}$,mb=$\frac{1}{2}$$\sqrt{2({a}^{2}+{c}^{2})-{b}^{2}}$,mc=$\frac{1}{2}$$\sqrt{2({a}^{2}+{b}^{2})-{c}^{2}}$.
分析 设BC边上的中线为AD,分别在△ABD和△ACD中,运用余弦定理,结合诱导公式,两式相加即可得到ma=$\frac{1}{2}$$\sqrt{2({b}^{2}+{c}^{2})-{a}^{2}}$,同理可证mb=$\frac{1}{2}$$\sqrt{2({a}^{2}+{c}^{2})-{b}^{2}}$,mc=$\frac{1}{2}$$\sqrt{2({a}^{2}+{b}^{2})-{c}^{2}}$.
解答 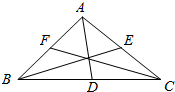 证明:设BC边上的中线为AD,
证明:设BC边上的中线为AD,
在△ABD中,c2=ma2+($\frac{1}{2}$a)2-2•$\frac{1}{2}$a•ma•cos∠ADB,①
在△ACD中,b2=ma2+($\frac{1}{2}$a)2-2•$\frac{1}{2}$a•ma•cos∠ADC,②
由于∠ADB+∠ADC=π,
则cos∠ADB+cos∠ADC=0,
①+②,可得c2+b2=2ma2+$\frac{1}{2}$a2,
即有ma=$\frac{1}{2}$$\sqrt{2({b}^{2}+{c}^{2})-{a}^{2}}$,
同理可证mb=$\frac{1}{2}$$\sqrt{2({a}^{2}+{c}^{2})-{b}^{2}}$,
mc=$\frac{1}{2}$$\sqrt{2({a}^{2}+{b}^{2})-{c}^{2}}$.
点评 本题考查余弦定理的运用,同时诱导公式的运用,考查化简运算能力,属于基础题.

练习册系列答案
相关题目
20.已知{an}为等差数列,a5是一个定值,Sn为{an}前n项的和,则下列各数也为定值的是( )
| A. | S5 | B. | S8 | C. | S9 | D. | S10 |