题目内容
【题目】已知![]() 为坐标原点,
为坐标原点,![]() 是抛物线
是抛物线![]() :
:![]() 的焦点,
的焦点,![]() 是抛物线
是抛物线![]() 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过![]() ,
,![]() ,
,![]() 三点的圆的圆心为
三点的圆的圆心为![]() .
.
(1)是否存在过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() ,使得抛物线
,使得抛物线![]() 上存在两点关于直线
上存在两点关于直线![]() 对称?若存在,求出
对称?若存在,求出![]() 的范围;若不存在,说明理由;
的范围;若不存在,说明理由;
(2)是否存在点![]() ,使得直线
,使得直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)不存在,理由见解析;(2)存在,![]()
【解析】
(1). 先假设存在,设直线![]() 的方程为
的方程为![]() ,若A,B两点关于直线
,若A,B两点关于直线![]() 对称,则直线
对称,则直线![]() 的方程为
的方程为![]() ,联立直线AB与抛物线方程,求A,B两点的中点N,再将N带入直线l中,在判断是否能求出k的范围;
,联立直线AB与抛物线方程,求A,B两点的中点N,再将N带入直线l中,在判断是否能求出k的范围;
(2). 将抛物线化为二次函数形:![]() ,利用导数的几何意义,求得切线MQ,结合Q点的宗坐标值,求得Q的横坐标;最后根据
,利用导数的几何意义,求得切线MQ,结合Q点的宗坐标值,求得Q的横坐标;最后根据![]() ,列出关于关于M点横坐标x的方程,并求解即可。
,列出关于关于M点横坐标x的方程,并求解即可。
(1)假设存在,设直线![]() 的方程为
的方程为![]() ,关于直线
,关于直线![]() 对称的两点
对称的两点![]() ,
,![]() ,由题意知
,由题意知![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
联立 消
消![]() 可得:
可得:![]() ,
,
![]() (※),
(※),
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() 中点
中点![]() ,由题意
,由题意![]() 在直线
在直线![]() 上,
上,
所以![]() ,即
,即![]() ,
,
代入(※)式可得:![]() ,即
,即![]() ,无实数解,故不存在符合题意的直线.
,无实数解,故不存在符合题意的直线.
(2)点![]() ,又
,又![]() ,设
,设![]() ,
,
![]() 变形为
变形为![]() ,所以
,所以![]() ,
,
因为直线![]() 为抛物线的切线,故
为抛物线的切线,故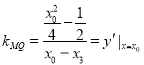 ,
,
解得![]() ,即
,即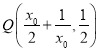 ,
,
又取![]() 中点
中点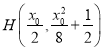 ,由垂径定理知
,由垂径定理知![]() ,
,
所以![]() 可得:
可得:![]() ,
,
解得![]() ,所以存在
,所以存在![]() 符合题意
符合题意

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目