题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,
,![]() ,点
,点![]() 为坐标平面内的一点,且
为坐标平面内的一点,且![]() ,
,![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() ,
,![]() 是椭圆
是椭圆![]() 上两个不同的点,直线
上两个不同的点,直线![]() ,
,![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() ,且
,且![]() .证明:直线
.证明:直线![]() 恒过定点,并求出该定点的坐标,
恒过定点,并求出该定点的坐标,
【答案】(1)![]() ;(2)证明见解析,定点
;(2)证明见解析,定点![]() .
.
【解析】
(1)设![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,运用两点间的距离公式和向量数量积的坐标表示,以及椭圆的离心率公式,解方程可得
,运用两点间的距离公式和向量数量积的坐标表示,以及椭圆的离心率公式,解方程可得![]() ,进而得到椭圆方程;
,进而得到椭圆方程;
(2)设![]() ,
,![]() ,判断直线
,判断直线![]() 的斜率不存在不成立,设直线
的斜率不存在不成立,设直线![]() 的方程为
的方程为![]() ,联立椭圆方程,运用判别式大于0,以及根与系数的关系,结合直线的斜率公式,化简整理,结合直线方程和恒过定点的求法,可得结果.
,联立椭圆方程,运用判别式大于0,以及根与系数的关系,结合直线的斜率公式,化简整理,结合直线方程和恒过定点的求法,可得结果.
解(1)设![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]()
则![]() ,
,![]()
由题意得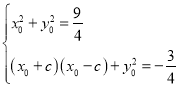
解得![]() .∴
.∴![]() .
.
又![]() ,∴
,∴![]()
∴![]()
∴所求椭圆![]() 的方程为:
的方程为:![]()
(2)由题可知直线![]() 的斜率存在,则设直线
的斜率存在,则设直线![]() 方程为
方程为![]() ,
,![]() ,
,![]() 坐标为
坐标为![]() ,
,![]()
解方程组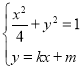
∴![]()
∴![]() ,
,![]()
又由![]() ,∴
,∴![]() ,
,
设直线![]() ,
,![]() 斜率分别为
斜率分别为![]() ,
,![]() ,则
,则![]()
∴![]()
即:![]()
![]()
∴![]()
∴![]()
化简得:![]()
得:![]() ,或
,或![]()
当![]() 时,
时,![]() ,过点(-2,0),不合题意(舍去)
,过点(-2,0),不合题意(舍去)
当![]() 时,
时,![]() ,过点
,过点![]() ,
,
∴直线![]() 恒过定点
恒过定点![]() .
.

【题目】![]() 年,某省将实施新高考,
年,某省将实施新高考,![]() 年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用
年秋季入学的高一学生是新高考首批考生,新高考不再分文理科,采用![]() 模式,其中语文、数学、外语三科为必考科目,满分各
模式,其中语文、数学、外语三科为必考科目,满分各![]() 分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物
分,另外,考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物![]() 门科目中自选
门科目中自选![]() 门参加考试(
门参加考试(![]() 选
选![]() ),每科目满分
),每科目满分![]() 分.为了应对新高考,某高中从高一年级
分.为了应对新高考,某高中从高一年级![]() 名学生(其中男生
名学生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分层抽样的方法从中抽取n名学生进行调查.
人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含女生![]() 人,求n的值及抽取到的男生人数;
人,求n的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下面表格是根据调查结果得到的![]() 列联表,请将下面的列联表补充完整,并判断是否有
列联表,请将下面的列联表补充完整,并判断是否有![]() 的把握认为选择科目与性别有关?说明你的理由;
的把握认为选择科目与性别有关?说明你的理由;
选择“物理” | 选择“历史” | 总计 | |
男生 | 10 | ||
女生 | 30 | ||
总计 |
(3)在抽取到的![]() 名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出
名女生中,在(2)的条件下,按选择的科目进行分层抽样,抽出![]() 名女生,了解女生对“历史”的选课意向情况,在这
名女生,了解女生对“历史”的选课意向情况,在这![]() 名女生中再抽取
名女生中再抽取![]() 人,求这
人,求这![]() 人中选择“历史”的人数为
人中选择“历史”的人数为![]() 人的概率.
人的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: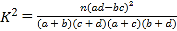 ,其中
,其中![]() )
)
【题目】“支付宝捐步”已经成为当下最热门的健身方式,为了了解是否使用支付宝捐步与年龄有关,研究人员随机抽取了5000名使用支付宝的人员进行调查,所得情况如下表所示:
50岁以上 | 50岁以下 | |
使用支付宝捐步 | 1000 | 1000 |
不使用支付宝捐步 | 2500 | 500 |
(1)由上表数据,能否有99.9%的把握认为是否使用支付宝捐步与年龄有关?
(2)55岁的老王在了解了捐步功能以后开启了自己的捐步计划,可知其在捐步的前5天,捐步的步数与天数呈线性相关.
第x天 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
步数 | 4000 | 4200 | 4300 | 5000 | 5500 |
(i)根据上表数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(ii)记由(i)中回归方程得到的预测步数为![]() ,若从5天中任取3天,记
,若从5天中任取3天,记![]() 的天数为X,求X的分布列以及数学期望.
的天数为X,求X的分布列以及数学期望.
附参考公式与数据: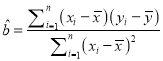 ,
,![]() ;K2=
;K2=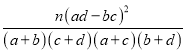 ;
;
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |