题目内容
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 上不单调,求a的取值范围;
上不单调,求a的取值范围;
(2)当![]() 时,记
时,记![]() 的两个零点是
的两个零点是![]()
①求a的取值范围;
②证明:![]() .
.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②证明见解析.
;②证明见解析.
【解析】
(1)先对函数求导整理得出![]() ,结合研究的区间,对
,结合研究的区间,对![]() 的范围进行讨论,结合函数在某个区间上不单调的条件,即既有增区间,又有减区间,即在区间上存在极值点,得到结果;
的范围进行讨论,结合函数在某个区间上不单调的条件,即既有增区间,又有减区间,即在区间上存在极值点,得到结果;
(2)①将函数在区间上有两个零点转化为方程![]() 有两个解,构造新函数,利用导数求得结果;
有两个解,构造新函数,利用导数求得结果;
②结合①,求得两个零点所属的区间,利用不等式的性质证得结果.
(1)因为![]() ,所以
,所以![]() ,
,
当![]() 时,可知
时,可知![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上单调递增,不合题意,
上单调递增,不合题意,
当![]() 时,即
时,即![]() 时,可知
时,可知![]() 时
时![]() ,
,![]() 单调减,
单调减,
当![]() 时
时![]() ,
,![]() 单调增,所以满足
单调增,所以满足![]() 在
在![]() 上不单调,
上不单调,
所以a的取值范围是![]() ;
;
(2)①令![]() ,得
,得![]() ,即
,即![]() 有两个解,
有两个解,
令![]() ,则
,则![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() ,
,
所以当![]() 时,记
时,记![]() 的两个零点,a的取值范围是
的两个零点,a的取值范围是![]() ;
;
②由①知![]() ,所以
,所以![]() ,
,
所以![]()

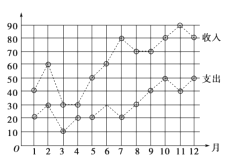
【题目】网络购物已经成为人们的一种生活方式.某购物平台为了给顾客提供更好的购物体验,为入驻商家设置了积分制度,每笔购物完成后,买家可以根据物流情况、商品质量等因素对商家做出评价,评价分为好评、中评和差评平台规定商家有50天的试营业时间,期间只评价不积分,正式营业后,每个好评给商家计1分,中评计0分,差评计![]() 分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
分,某商家在试营业期间随机抽取100单交易调查了其商品的物流情况以及买家的评价情况,分别制成了图1和图2.
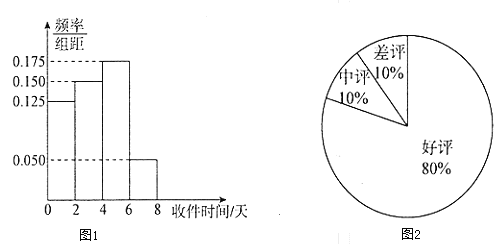
(1)通常收件时间不超过四天认为是物流迅速,否则认为是物流迟缓;
请根据题目所给信息完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“获得好评”与物流速度有关?
的把握认为“获得好评”与物流速度有关?
好评 | 中评或差评 | 合计 | |
物流迅速 | |||
物流迟缓 | 30 | ||
合计 |
(2)从正式营业开始,记商家在每笔交易中得到的评价得分为![]() .该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
.该商家将试营业50天期间的成交情况制成了频数分布表(表1),以试营业期间成交单数的频率代替正式营业时成交单数发生的概率.
表1
成交单数 | 36 | 30 | 27 |
天数 | 10 | 20 | 20 |
(Ⅰ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)平台规定,当积分超过10000分时,商家会获得“诚信商家”称号,请估计该商家从正式营业开始,1年内(365天)能否获得“诚信商家”称号
附: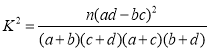
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】垃圾分类是对垃圾进行有效处置的一种科学管理方法.太原市为推进这项工作的实施,开展了“垃圾分类进小区”的评比活动.现有甲、乙两个小区采取不同的宣传与倡导方式对各自小区居民进行了有关垃圾分类知识的培训,并参加了评比活动,评委会随机从两个小区各选出20户家庭进行评比打分,每户成绩满分为100分,评分后得到如下茎叶图.
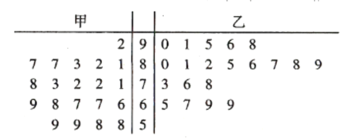
(1)依茎叶图判断哪个小区的平均分高?
(2)现从甲小区不低于80分的家庭中随机抽取两户,求分数为87的家庭至少有一户被抽中的概率;
(3)如果规定分数不低于85分的家庭为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为得分是否优秀与小区宣传培训方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为得分是否优秀与小区宣传培训方式有关?”
甲 | 乙 | 合计 | |
优秀 |
|
| |
不优秀 |
|
| |
合计 |
参考公式和数据: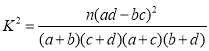 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |