题目内容
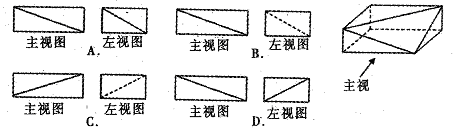
用单位正方块搭一个几何体,使它的主视图和俯视图如右图所示,则该几何体的体积
的最小值与最大值分别为( )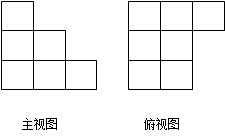
A.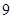 与 与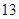 | B. 与 与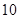 |
C.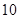 与 与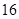 | D.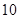 与 与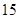 |
C
解析试题分析:在俯视图可知最底层要有7个正方体,结合正视图可知要在第一列至少加2个使其上下排列,在第二列至少加1个,因此至少10个正方体,最左在第一列各排都加2个共6个,在第二列的各排都加1个,共3个,所以最多7+9=16个,所以体积的最小值最大值分别为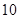 与
与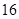
考点:三视图
点评:本题由三视图联想空间几何体的特征,在俯视图满足的条件下调整小正方体的个数使其满足正视图,从而得到体积的最值,求解本题要求学生要有一定的空间想象能力

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
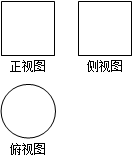
某几何体的三视图如图所示,则它的体积是( )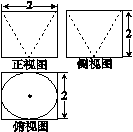
A.8- | B.8- | C.8-2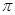 | D. |
一个几何体的正视图为一个四边形,则这个几何体可能是下列几何体中的( )
①圆锥 ②圆柱 ③三棱锥 ④四棱柱
| A.①② | B.②③ | C.①④ | D.②④ |
已知一个几何体的三视图如右图,则该几何体的体积为 ( ) 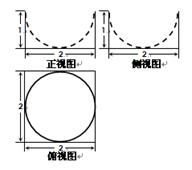
A. |
B.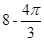 |
C. |
D.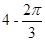 |
某空间几何体的三视图如图所示,该空间几何体的体积是( )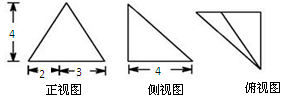
A.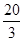 | B.10 | C.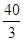 | D.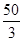 |
如图为一几何体的三视图,则该几何体体积为( )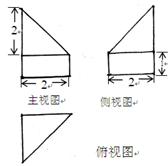
A. |
| B.6 |
C. |
D.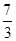 |
已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为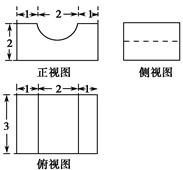
A.24-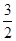 π π | B.24-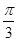 | C.24-π | D.24-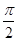 |