题目内容
(3分)(2011•重庆)下列区间中,函数f(x)=|lg(2﹣x)|在其上为增函数的是( )
| A.(﹣∞,1] | B.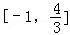 | C.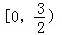 | D.(1,2) |
D
解析试题分析:根据零点分段法,我们易将函数f(x)=|lg(2﹣x)|的解析式化为分段函数的形式,再根据复合函数“同增异减”的原则我们易求出函数的单调区间进而得到结论.
解:∵f(x)=|lg(2﹣x)|,
∴f(x)=
根据复合函数的单调性我们易得
在区间(﹣∞,1]上单调递减
在区间(1,2)上单调递增
故选D
点评:本题考查的知识点是对数函数的单调性与特殊点,其中根据“同增异减”的原则确定每一段函数的单调性是解答本题的关键.

练习册系列答案
相关题目
设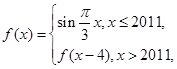 则f(2 016)=( )
则f(2 016)=( )
A.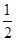 | B.-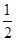 | C.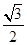 | D.-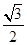 |
(5分)(2011•陕西)方程|x|=cosx在(﹣∞,+∞)内( )
| A.没有根 | B.有且仅有一个根 | C.有且仅有两个根 | D.有无穷多个根 |
已知函数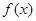 在[0,+∞]上是增函数,
在[0,+∞]上是增函数,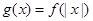 ,若
,若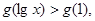 则
则 的取值范围是( )
的取值范围是( )
A.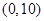 | B.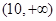 |
C.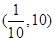 | D.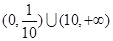 |
已知函数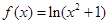 的值域为
的值域为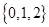 ,则满足这样条件的函数的个数有( )个.
,则满足这样条件的函数的个数有( )个.
| A.8 | B.9 | C.26 | D.27 |
下列函数中,不满足f(2x)=2f(x)的是( )
| A.f(x)=|x| | B.f(x)=x-|x| |
| C.f(x)=x+1 | D.f(x)=-x |
(2014·宜昌模拟)若定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在区间[0,1]上单调递减,则( )
A.f(2)<f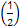 <f(1) <f(1) | B.f(1)<f(2)<f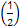 |
C.f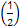 <f(2)<f(1) <f(2)<f(1) | D.f(1)<f <f(2) <f(2) |