题目内容
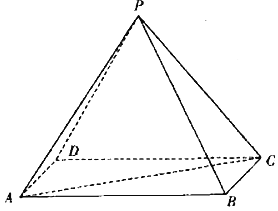
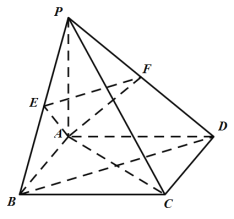
【题目】如图,已知四棱锥![]() 的底面
的底面![]() 为棱形,且
为棱形,且![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 面
面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先利用线面垂直的性质证明![]() ,再由菱形的性质可得
,再由菱形的性质可得![]() ,根据线面垂直的判定定理可得结果;(2)建立空间直角坐标系, 取
,根据线面垂直的判定定理可得结果;(2)建立空间直角坐标系, 取![]() 的中点
的中点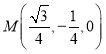 ,连
,连![]() ,易证
,易证![]() 面
面![]() ,可得平面
,可得平面![]() 的一个法向量为
的一个法向量为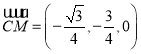 ,利用向量垂直数量积为零求出平面
,利用向量垂直数量积为零求出平面![]() 的法向量,利用空间向量加角余弦公式可求出二面角
的法向量,利用空间向量加角余弦公式可求出二面角![]() 的余弦值.
的余弦值.
(1)∵![]() 平面
平面![]()
∴![]()
又∵在菱形![]() 中,对角线为
中,对角线为![]() 与
与![]()
∴![]()
又∵![]()
∴![]() 面
面![]()
(2)

平面![]() 内,过
内,过![]() 作直线与
作直线与![]() 垂直,建立如图所示的空间直角坐标系,
垂直,建立如图所示的空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,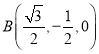 ,
,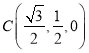 ,
,
∴中点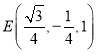 ,中点
,中点![]()
则取![]() 的中点
的中点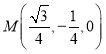 ,连
,连![]() ,
,
则![]() ,
,
所以 ![]() 面
面![]() ,
,
所以面![]() 的一个法向量为
的一个法向量为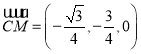 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
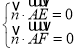 ∴
∴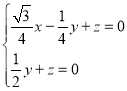 令
令![]() ,则
,则![]() ,
,![]() ∴
∴![]()
令二面角![]() 的平面角为
的平面角为![]() ,易知该二面角为锐角
,易知该二面角为锐角
∴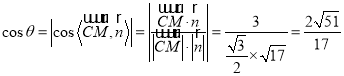 .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
【题目】有两种理财产品![]() 和
和![]() ,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
,投资这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
产品![]() :
:
投资结果 | 获利 | 不赔不赚 | 亏损 |
概率 |
|
|
|
注:![]()
(1)若甲、乙两人分别选择了产品![]() 投资,一年后他们中至少有一人获利的概率大于
投资,一年后他们中至少有一人获利的概率大于![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若丙要将20万元人民币投资其中一种产品,以一年后的投资收益的期望值为决策依据,则丙选择哪种产品投资较为理想.