题目内容
已知函数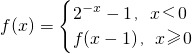 则满足f(x0)=1的实数x0的集合是________.
则满足f(x0)=1的实数x0的集合是________.
{x|x≥-1且x∈z}
分析:当x≥0时,函数的周期为1,然后利用函数的周期性确定方程的根.
解答: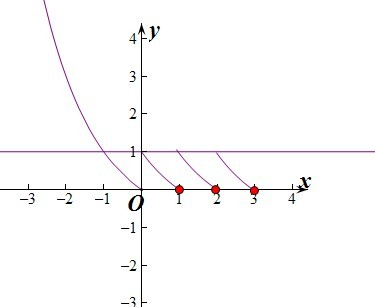 解:当x≥0时,f(x)=f(x-1),所以函数的周期是1.
解:当x≥0时,f(x)=f(x-1),所以函数的周期是1.
当0≤x<1时,则-1≤x-1<0,
此时f(x)=f(x-1)=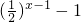 .
.
当x<0时,由f(x0)=1
得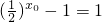 ,即
,即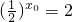 ,解得x0=-1.
,解得x0=-1.
因为当x≥0时,f(x)=f(x-1),所以函数的周期是1.
所以x0=0,1,2,…,
所以满足f(x0)=1的实数x0的集合是{x|x≥-1且x∈z}.
故答案为:{x|x≥-1且x∈z}.
点评:本题主要考查函数的周期性的应用,利用数形结合是解决本题的关键.
分析:当x≥0时,函数的周期为1,然后利用函数的周期性确定方程的根.
解答:
 解:当x≥0时,f(x)=f(x-1),所以函数的周期是1.
解:当x≥0时,f(x)=f(x-1),所以函数的周期是1.当0≤x<1时,则-1≤x-1<0,
此时f(x)=f(x-1)=
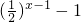 .
.当x<0时,由f(x0)=1
得
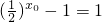 ,即
,即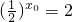 ,解得x0=-1.
,解得x0=-1.因为当x≥0时,f(x)=f(x-1),所以函数的周期是1.
所以x0=0,1,2,…,
所以满足f(x0)=1的实数x0的集合是{x|x≥-1且x∈z}.
故答案为:{x|x≥-1且x∈z}.
点评:本题主要考查函数的周期性的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
已知函数
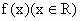 ,满足f(-x)=f(x),则下列各点中必在函数y=f(x)图象上的是
,满足f(-x)=f(x),则下列各点中必在函数y=f(x)图象上的是
[
]|
A .(-a,f(a)) |
B .(-a,-f(a)) |
|
C .(-a,-f(-a)) |
D .(a,-f(a)) |
已知函数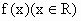 ,满足f(-x)=f(x),则下列各点中必在函数y=f(x)图象上的是
,满足f(-x)=f(x),则下列各点中必在函数y=f(x)图象上的是
[ ]
|
A.(-a,f(a)) |
B.(-a,-f(a)) |
|
C.(-a,-f(-a)) |
D.(a,-f(a)) |
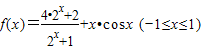 ,且f(x)存在最大值M和最小值N,则M、N一定满足( )
,且f(x)存在最大值M和最小值N,则M、N一定满足( )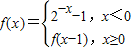 则满足f(x)=1的实数x的集合是 .
则满足f(x)=1的实数x的集合是 .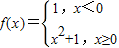 则满足不等式f(1-x2)>f(2x)的x的取值范围是( )
则满足不等式f(1-x2)>f(2x)的x的取值范围是( )