题目内容
已知函数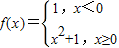 则满足不等式f(1-x2)>f(2x)的x的取值范围是( )
则满足不等式f(1-x2)>f(2x)的x的取值范围是( )A.(0,1)
B.[0,1]
C.
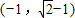
D.
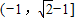
【答案】分析:由题意可得 f(x)在[0,+∞)上是增函数,而x<0时,f(x)=1,故满足不等式f(1-x2)>f(2x)的x需满足 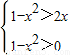 ,解出x即可.
,解出x即可.
解答:解:由题意可得 f(x)在[0,+∞)上是增函数,而x<0时,f(x)=1,
故满足不等式f(1-x2)>f(2x)的x需满足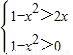 ,即
,即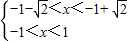 ,
,
解得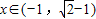 ,
,
故选:C.
点评:本题考查分段函数的单调性,利用单调性解不等式,考查利用所学知识分析问题解决问题的能力.
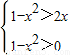 ,解出x即可.
,解出x即可.解答:解:由题意可得 f(x)在[0,+∞)上是增函数,而x<0时,f(x)=1,
故满足不等式f(1-x2)>f(2x)的x需满足
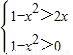 ,即
,即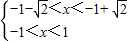 ,
,解得
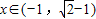 ,
,故选:C.
点评:本题考查分段函数的单调性,利用单调性解不等式,考查利用所学知识分析问题解决问题的能力.

练习册系列答案
相关题目
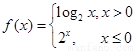 则满足不等式
则满足不等式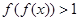 的x的取值范围是
的x的取值范围是 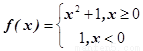 ,则满足不等式
,则满足不等式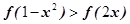 的x的范围是____
____
的x的范围是____
____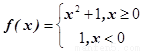 ,则满足不等式
,则满足不等式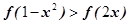 的x的范围是____
____
的x的范围是____
____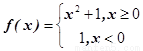 ,则满足不等式
,则满足不等式 的x的范围是____
____
的x的范围是____
____ ,则满足不等式
,则满足不等式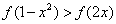 的x的范围是__▲___。
的x的范围是__▲___。