题目内容
(09年湖北八校联考理)(12分)
已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若![]() 对满足
对满足![]() 的任意实数
的任意实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围(这里
的取值范围(这里![]() 是自然对数的底数);
是自然对数的底数);
(Ⅲ)求证:对任意正数![]() 、
、![]() 、
、![]() 、
、![]() ,恒有
,恒有
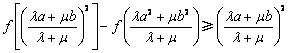
![]() .
.
解析:(Ⅰ)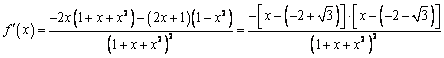
∴![]() 的增区间为
的增区间为![]() ,
,![]() 减区间为
减区间为![]() 和
和![]() .
.
极大值为![]() ,极小值为
,极小值为![]() .…………4′
.…………4′
(Ⅱ)原不等式可化为![]() 由(Ⅰ)知,
由(Ⅰ)知,![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
∴![]() 的最大值为
的最大值为![]() ,由恒成立的意义知道
,由恒成立的意义知道![]() ,从而
,从而![]() …8′
…8′
(Ⅲ)设![]()
则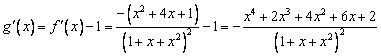 .
.
∴当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是减函数,
上是减函数,
又当![]() 、
、![]() 、
、![]() 、
、![]() 是正实数时,
是正实数时,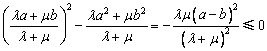
∴![]() .
.
由![]() 的单调性有:
的单调性有: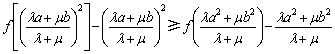 ,
,
即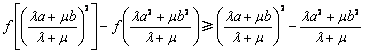 .…………12′
.…………12′

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目