Question

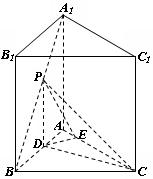
（09年湖北八校联考理）（12分）如图，已知正三棱柱各棱长都为，为棱上的动点。

（Ⅰ）试确定的值，使得；

（Ⅱ）若，求二面角的大小；

（Ⅲ）在（Ⅱ）的条件下，求点到面的距离。

Answer 1

解析：【法一】（Ⅰ）当时，作在上的射影. 连结.

则平面，∴，∴是的中点，又，∴也是的中点，

即.  反之当时，取的中点，连接、.

∵为正三角形，∴.   由于为的中点时，

∵平面，∴平面，∴.……4′

（Ⅱ）当时，作在上的射影. 则底面.

作在上的射影，连结，则.

∴为二面角的平面角。

又∵，∴，∴.

∴，又∵，∴.

∴，∴的大小为.…8′

（Ⅲ）设到面的距离为，则，∵，∴平面,

∴即为点到平面的距离，

又，∴.

即，解得.即到面的距离为.12′

【法二】以为原点，为轴，过点与垂直的直线为轴，

为轴，建立空间直角坐标系，如图所示，

设，则、、.

（Ⅰ）由得，

即，∴，即为的中点，

也即时，.…………4′

（Ⅱ）当时，点的坐标是.  取.

则，.

∴是平面的一个法向量。

又平面的一个法向量为.

∴，∴二面角的大小是.……8′

（Ⅲ）设到面的距离为，则，∴到面的距离为.