题目内容
【题目】已知正四面体P－ABC的棱长均为a，O为正四面体P－ABC的外接球的球心，过点O作平行于底面ABC的平面截正四面体P－ABC，得到三棱锥P－A1B1C1和三棱台ABC－A1B1C1，那么三棱锥P－A1B1C1的外接球的表面积为________.
【答案】
【解析】
先求正四面体P－ABC的高和外接球半径
，再根据正四面体P－ABC与三棱锥P－A1B1C1相似，用高求出相似比，求得三棱锥P－A1B1C1的外接球的半径，从而求得外接球的表面积.
作示意图如图所示,
为
的中心，
为三角形
的中心，
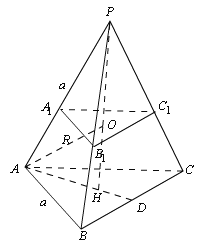
则
，
，则正四面体P－ABC的高
＝
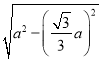a，则R2＝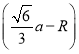
2＋
2，
解得R＝
a. 三棱锥P－A1B1C1的高为
，
，∴
∶
＝3∶4，
所以三棱锥P－A1B1C1的外接球的表面积为4π×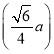
2×
2＝
a2.
故答案为：
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
