题目内容
【题目】在平面直角坐标系![]() 中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (t为参数),
(t为参数),![]() ,点A为直线
,点A为直线![]() 与曲线C在第二象限的交点,过O点的直线
与曲线C在第二象限的交点,过O点的直线![]() 与直线
与直线![]() 互相垂直,点B为直线
互相垂直,点B为直线![]() 与曲线C在第三象限的交点.
与曲线C在第三象限的交点.
(1)写出曲线C的直角坐标方程及直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() .(
.(![]() );(2)
);(2)![]() .
.
【解析】
(1)根据![]() ,
,![]() 得出曲线C的直角坐标方程,消掉参数
得出曲线C的直角坐标方程,消掉参数![]() 得出直线
得出直线![]() 的普通方程;
的普通方程;
(2)根据极坐标中极径的意义以及三角形的面积公式,即可得出![]() 的面积.
的面积.
(1)曲线C的极坐标方程化为![]() ,
,![]() ,
,![]()
![]() 曲线C的直角坐标方程为
曲线C的直角坐标方程为![]() .
.
直线![]() 的普通方程为
的普通方程为![]() .(
.(![]() )
)
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,(
,(![]() ),则
),则![]()
射线![]() 的极坐标方程为
的极坐标方程为![]() ,(
,(![]() ),则
),则
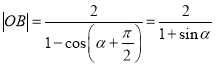
由![]() 得
得![]() ,
,![]() ,解得:
,解得:![]()
故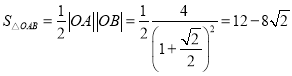

【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元).这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据y(单位:十亿元),绘制如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额y | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示
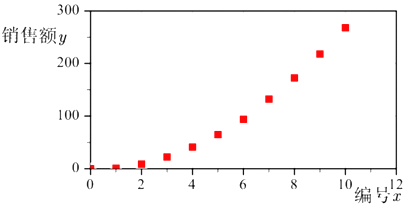
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为销售额
哪一个适宜作为销售额![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及如表中的数据,建立![]() 关于
关于![]() 的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
的回归方程,并预测2020年天猫双十一销售额;(注:数据保留小数点后一位)
(3)把销售超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率.
参考数据:![]()
|
|
|
|
|
|
参考公式:
对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别
的斜率和截距的最小二乘估计公式分别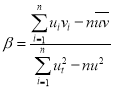 ,
,![]() .
.
【题目】某工厂为了提高生产效率,对生产设备进行了技术改造,为了对比技术改造后的效果,采集了技术改造前后各20次连续正常运行的时间长度(单位:天)数据,整理如下:
改造前:19,31,22,26,34,15,22,25,40,35,18,16,28,23,34,15,26,20,24,21
改造后:32,29,41,18,26,33,42,34,37,39,33,22,42,35,43,27,41,37,38,36
(1)完成下面的列联表,并判断能否有99%的把握认为技术改造前后的连续正常运行时间有差异?
超过30 | 不超过30 | |
改造前 | ||
改造后 |
(2)工厂的生产设备的运行需要进行维护,工厂对生产设备的生产维护费用包括正常维护费,保障维护费两种.对生产设备设定维护周期为T天(即从开工运行到第kT天,k∈N*)进行维护.生产设备在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产设备能连续运行,则只产生一次正常维护费,而不会产生保障维护费;若生产设备不能连续运行,则除产生一次正常维护费外,还产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产设备一个生产周期(以120天计)内的维护方案:T=30,k=1,2,3,4.以生产设备在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及均值.
附: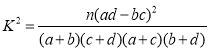
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
