题目内容

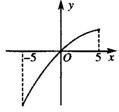精英家教网函数y=f（x），x∈[-5，5]的图象如图所示，该曲线在原点处的切线的方程为y=x，且导函数f′（x）是减函数．给出下列四个命题：
①A，B是该图象上的任意两点，那么直线AB的斜率kAB∈（0，1）；
②点P是该图象在第一象限内的部分上的点，那么直线OP的斜率kOP∈（0，1）；
③对于?x1，x2∈[-5，5]，f（x1）+f（x2）≤2f（
x1+x2
2
）恒成立；
④对于?x∈[-5，5]，f（x）≤x．
其中所有真命题的序号是（　　）
A、①②③B、②③④
C、②④D、①③
分析：对于①A，B是该图象上的任意两点，直线AB的斜率可以用AB中点对应的横坐标对应到图象上点的切线斜率近似代替，根据函数的导数是一个减函数，知当x＜0时f′（x）＞f′（0）=1，故①不正确；再结合选项，说明应在B、C当中选一个，问题的焦点集中到③这个命题是否正确了．利用函数图象的凹凸性不难发现命题③是正确的，这样就可以选到正确答案了．
解答：解：先看命题①：若A，B是该图象上的任意两点，直线AB的斜率可以用AB中点对应的横坐标对应到图象上点的切线斜率近似代替，
由已知条件曲线在原点处的切线的方程为y=x，说明f′（0）=1，再根据函数的导数是一个减函数知
当x＜0时f′（x）＞f′（0）=1，说明存在-5＜x＜0时直线AB的斜率kAB＞1，故①不正确；
再结合选项：只有B、C当中没有认为①正确，说明应在B、C当中选一个，
问题的焦点集中到③这个命题是否正确了．
利用函数图象的凹凸性：函数f（x）是一个凸函数，说明满足不等式：f(
x1+x2
2
) ≥
1
2
(f(x1)+f(x2) )
对照一下命题③，说明命题③是正确的，因此可得正确答案为②③④．
故选B
点评：本题考查了利用导数研究函数的图象、函数图象的凹凸性和函数恒成立等问题，综合性较强，是一道难题．此问题还着重考查学生观察图形，分析问题和解决问题的能力，不失为一道优良的考题．
练习册系列答案
相关题目
（2013•黄埔区一模）对于函数y=f（x）与常数a，b，若f（2x）=af（x）+b恒成立，则称（a，b）为函数f（x）的一个“P数对”；若f（2x）≥af（x）+b恒成立，则称（a，b）为函数f（x）的一个“类P数对”．设函数f（x）的定义域为R+，且f（1）=3．
（1）若（1，1）是f（x）的一个“P数对”，求f（2n）（n∈N*）；
（2）若（-2，0）是f（x）的一个“P数对”，且当x∈[1，2）时f（x）=k-|2x-3|，求f（x）在区间[1，2n）（n∈N*）上的最大值与最小值；
（3）若f（x）是增函数，且（2，-2）是f（x）的一个“类P数对”，试比较下列各组中两个式子的大小，并说明理由．
①f（2-n）与2-n+2（n∈N*）；
②f（x）与2x+2（x∈（0，1]）．
（选作题）定义在（-1，1）上的函数y=f（x）满足：对任意x，y∈（-1，1）都有f(x)+f(y)=f(
x+y
1+xy
)．
（1）判断函数f（x）的奇偶性，并证明；
（2）如果当x∈（-1，0）时，有f（x）＞0，求证：f（x）在（-1，1）上是单调递减函数；
（3）在（2）的条件下解不等式：f(x+
1
2
)+f(
1
1-x
)＞0．
（2011•顺义区二模）对于定义域分别为M，N的函数y=f（x），y=g（x），规定：
函数h(x)=
f(x)•g(x)，当x∈M且x∈N
f(x)，当x∈M且x∉N
g(x)，当x∉M且x∈N

（1）若函数f(x)=
1
x+1
，g(x)=x2+2x+2，x∈R，求函数h（x）的取值集合；
（2）若f（x）=1，g（x）=x2+2x+2，设bn为曲线y=h（x）在点（an，h（an））处切线的斜率；而{an}是等差数列，公差为1（n∈N*），点P1为直线l：2x-y+2=0与x轴的交点，点Pn的坐标为（an，bn）．求证：
1
|P1P2|2
+
1
|P1P3|2
+…+
1
|P1Pn|2
＜
2
5
；
（3）若g（x）=f（x+α），其中α是常数，且α∈[0，2π]，请问，是否存在一个定义域为R的函数y=f（x）及一个α的值，使得h（x）=cosx，若存在请写出一个f（x）的解析式及一个α的值，若不存在请说明理由．
（2012•浦东新区二模）已知函数y=f（x），x∈D，如果对于定义域D内的任意实数x，对于给定的非零常数m，总存在非零常数T，恒有f（x+T）＞m•f（x）成立，则称函数f（x）是D上的m级类增周期函数，周期为T．若恒有f（x+T）=m•f（x）成立，则称函数f（x）是D上的m级类周期函数，周期为T．
（1）试判断函数f（x）=log
12
(x-1)是否为（3，+∞）上的周期为1的2级类增周期函数？并说明理由；
（2）已知函数f（x）=-x2+ax是[3，+∞）上的周期为1的2级类增周期函数，求实数a的取值范围；
（3）下面两个问题可以任选一个问题作答，如果你选做了两个，我们将按照问题（Ⅰ）给你记分．
（Ⅰ）已知T=1，y=f（x）是[0，+∞）上m级类周期函数，且y=f（x）是[0，+∞）上的单调递增函数，当x∈[0，1）时，f（x）=2x，求实数m的取值范围．
（Ⅱ）已知当x∈[0，4]时，函数f（x）=x2-4x，若f（x）是[0，+∞）上周期为4的m级类周期函数，且y=f（x）的值域为一个闭区间，求实数m的取值范围．
（2009•卢湾区一模）将奇函数的图象关于原点（即（0，0））对称这一性质进行拓广，有下面的结论：
①函数y=f（x）满足f（a+x）+f（a-x）=2b的充要条件是y=f（x）的图象关于点（a，b）成中心对称．
②函数y=f（x）满足F（x）=f（x+a）-f（a）为奇函数的充要条件是y=f（x）的图象关于点（a，f（a））成中心对称（注：若a不属于x的定义域时，则f（a）不存在）．
利用上述结论完成下列各题：
（1）写出函数f（x）=tanx的图象的对称中心的坐标，并加以证明．
（2）已知m（m≠-1）为实数，试问函数f(x)=
x+m
x-1
的图象是否关于某一点成中心对称？若是，求出对称中心的坐标并说明理由；若不是，请说明理由．
（3）若函数f(x)=(x-
2
3
)(|x+t|+|x-3|)-4的图象关于点(
2
3
，f(
2
3
))成中心对称，求t的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网