题目内容
定义在R上的偶函数 满足
满足 ,且在[-3,-2]上是减函数,若
,且在[-3,-2]上是减函数,若 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则 与
与 的大小关系为 ;
的大小关系为 ;
 满足
满足 ,且在[-3,-2]上是减函数,若
,且在[-3,-2]上是减函数,若 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则 与
与 的大小关系为 ;
的大小关系为 ;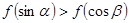
解:∵定义在R上的偶函数f(x)满足条件f(x+2)=f(x),且在[-3,-2]上递减,
∴f(x)在[-1,0]减,在[0,1]增,
又α,β是锐角三角形的两内角,
∴α+β>π/ 2 ,即α>π /2 -β,β>π/ 2 -α
∴0<sin(π /2 -β)<sinα<1,0<sin(π /2 -α)<sinβ<1
∴0<cosβ<sinα<1,0<cosα<sinβ<1
∴f(cosβ)<f(sinα),f(cosα)<f(sinβ),故填写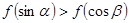
∴f(x)在[-1,0]减,在[0,1]增,
又α,β是锐角三角形的两内角,
∴α+β>π/ 2 ,即α>π /2 -β,β>π/ 2 -α
∴0<sin(π /2 -β)<sinα<1,0<sin(π /2 -α)<sinβ<1
∴0<cosβ<sinα<1,0<cosα<sinβ<1
∴f(cosβ)<f(sinα),f(cosα)<f(sinβ),故填写
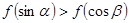

练习册系列答案
相关题目
 ,则
,则 ”的逆否命题为“若
”的逆否命题为“若 ”;
”; ,则
,则
 为假命题,则
为假命题,则 ,
, 均为假命题;
均为假命题; 的充分不必要条件.
的充分不必要条件. :
: 和
和 是方程
是方程 的两个实数根,不等式
的两个实数根,不等式 对任意实数
对任意实数 ,
, 恒成立,命题
恒成立,命题 :只有一个实数
:只有一个实数 满足不等式
满足不等式 ,若
,若 的取值范围是 .
的取值范围是 .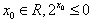 ”的否定是:“不存在
”的否定是:“不存在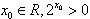 ”;
”;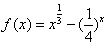 的零点在区间
的零点在区间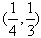 内;
内; 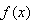 满足
满足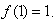 且
且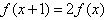 ,则
,则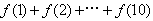 =1023;
=1023;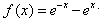 切线斜率的最大值是2.
切线斜率的最大值是2. ; p2:|a+b|>1?θ∈
; p2:|a+b|>1?θ∈
 ; p4:|a-b|>1?θ∈
; p4:|a-b|>1?θ∈ .
.