题目内容
【题目】已知数列{an}为等比数列，Sn为其前n项和，且 
，则t=（ ）
A.
B.
C.
D.
【答案】C
【解析】解：∵数列{an}为等比数列，Sn为其前n项和，且 
， ∴a1=S1=2017×2016﹣2018t，
a2=S2﹣S1=（2017×20162﹣2018t）﹣（2017×2016﹣2018t）=2017×2016×2015，
a3=S3﹣S2=（2017×20162﹣2018t）﹣（2017×20162﹣2018t）=2017×20162×2015，
∵等比数列{an}中， 
，
∴（2017×2016×2015）2=（2017×2016﹣2018t）×（2017×20162×2015），
解得t= 
．
故选：C．
【考点精析】本题主要考查了等比数列的通项公式（及其变式）的相关知识点，需要掌握通项公式：
才能正确解答此题．
练习册系列答案
相关题目
【题目】国家实施二孩放开政策后，为了了解人们对此政策持支持态度是否与年龄有关，计生部门将已婚且育有一孩的居民分成中老年组（45岁以上，含45岁）和中青年组（45岁以下，不含45岁）两个组别，每组各随机调查了50人，对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图，如图所示：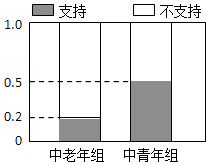 
支持 | 不支持 | 合计 | |
中老年组 | 50 | ||
中青年组 | 50 | ||
合 计 | 100 |
（1）根据以上信息完成2×2列联表；
（2）是否有99%以上的把握认为人们对此政策持支持态度与年龄有关？
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
附： 
．
