题目内容
6.已知A={y|y=x2-2x-1,x∈R},B={x|-2≤x<8},则集合A与B的关系是B⊆A.分析 首先,化简集合A,就是求解函数y=x2-2x-1,x∈R的值域,然后,利用集合之间的基本关系进行判断即可.
解答 解:由集合A得y=x2-2x-1=(x-1)2-2,x∈R
∴y≥-2,
∴A={y|y≥-2},
∵B={x|-2≤x<8},
∴B⊆A,
故答案为:B⊆A.
点评 本题重点考查集合之间的基本关系,属于基础题,注意落实集合M的元素取值情形.

练习册系列答案
相关题目
16.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(c,0)关于直线y=$\frac{b}{c}$x的对称点Q在椭圆上,则椭圆的离心率是( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{3}{5}$ |
11.已知偶函数f(x)对于任意x∈R都有f(x+1)=-f(x),且f(x)在区间[0,2]上是递增的,则f(-6.5),f(-1),f(0)的大小关系是( )
| A. | f(0)<f(-6.5)<f(-1) | B. | f(-6.5)<f(0)<f(-1) | C. | f(-1)<f(-6.5)<f(0) | D. | f(-1)<f(0)<f(-6.5) |
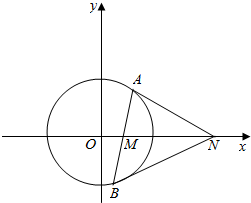 如图,已知圆O:x2+y2=r2(r>0),动直线l过点M(1,0)交圆O于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点N在x轴上,若点B的坐标为(0,-r),则点A的横坐标为$\frac{8}{5}$.
如图,已知圆O:x2+y2=r2(r>0),动直线l过点M(1,0)交圆O于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点N在x轴上,若点B的坐标为(0,-r),则点A的横坐标为$\frac{8}{5}$.