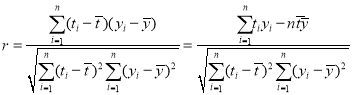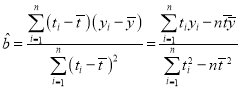题目内容
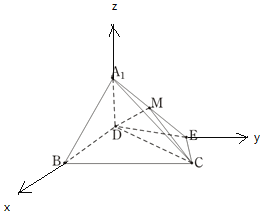
【题目】如图![]() ,已知
,已知![]() 是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足
是边长为6的等边三角形,点D、E分别是边AB、AC上的点,且满足![]() ,如图
,如图![]() ,将
,将![]() 沿DE折成四棱锥
沿DE折成四棱锥![]() ,且有平面
,且有平面![]() 平面BCED.
平面BCED.

![]() 求证:
求证:![]() 平面BCED;
平面BCED;
![]() 记
记![]() 的中点为M,求二面角
的中点为M,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
![]() 由余弦定理得
由余弦定理得![]() ,由色股定理得
,由色股定理得![]() ,由此能证明
,由此能证明![]() 平面BCED.
平面BCED.
![]() 由
由![]() 平面BCED,且
平面BCED,且![]() ,以D为原点建立空间直角坐标系,利用向量法能求出二面角
,以D为原点建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
证明:![]() 依题意
依题意![]() ,
,![]() ,
,![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 平面
平面![]() 平面BCDE,
平面BCDE,
![]() 平面BCED.
平面BCED.
![]() 由
由![]() 得
得![]() 平面BCED,且
平面BCED,且![]() ,
,
以D为原点建立空间直角坐标系,
则![]() 0,
0,![]() ,
,![]() ,
,![]() 0,
0,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 0,
0,![]() ,
,
设平面MDC的法向量![]() y,
y,![]() ,
,
则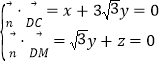 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() y,
y,![]() ,
,
则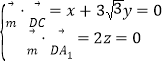 ,取
,取![]() ,得
,得![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]() .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】已知无穷等比数列![]() 的首项、公比均为
的首项、公比均为![]() .
.
(1)试求无穷等比子数列![]() 各项的和;
各项的和;
(2)是否存在数列![]() 的一个无穷等比子数列,使得它各项的和为
的一个无穷等比子数列,使得它各项的和为![]() ?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
?若存在,求出所有满足条件的子数列的通项公式;若不存在,请说明理由.
【题目】某工厂连续6天对新研发的产品按事先拟定的价格进行试销,得到一组数据![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
试销价 | 9 | 11 | 10 | 12 | 13 | 14 |
产品销量 | 40 | 32 | 29 | 35 | 44 |
|
(1)试根据4月2日、3日、4日的三组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测4月6日的产品销售量
,并预测4月6日的产品销售量![]() ;
;
(2)若选取两组数据确定回归方程,求选取得两组数据恰好是不相邻两天的事件![]() 的概率.
的概率.
参考公式:![]()
其中
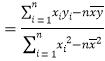 ,
,![]()