题目内容
【题目】已知定点![]() ,动点
,动点![]() 在圆
在圆![]() :
:![]() 上,线段
上,线段![]() 的中垂线为直线
的中垂线为直线![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,动点
,动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() 在第二象限,且相应的直线
在第二象限,且相应的直线![]() 与曲线
与曲线![]() 和抛物线
和抛物线![]() :
:![]() 都相切,求点
都相切,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)首先看动点![]() 有什么性质?由中垂线得
有什么性质?由中垂线得![]() ,从而
,从而![]() ,是常数,因此
,是常数,因此![]() 点轨迹是椭圆,且
点轨迹是椭圆,且![]() 是焦点,因此易得
是焦点,因此易得![]() 的方程;(2)直线
的方程;(2)直线![]() 是椭圆和抛物线的公切线,因此设
是椭圆和抛物线的公切线,因此设![]() 方程为
方程为![]() ,由它与椭圆相切(代入椭圆方程,判别式为0)可得一个等式
,由它与椭圆相切(代入椭圆方程,判别式为0)可得一个等式![]() ,同样由它与抛物线相切又可得一个等式
,同样由它与抛物线相切又可得一个等式![]() ,联立后可解得
,联立后可解得![]() ,注意
,注意![]() 在第二象限,可得唯一解,再
在第二象限,可得唯一解,再![]() 关于直线
关于直线![]() 对称可求得
对称可求得![]() 点坐标.
点坐标.
试题解析:(1)圆![]() 的圆心为
的圆心为![]() ,半径
,半径![]() ,连结
,连结![]() ,
,
∵![]() 在
在![]() 的中垂线
的中垂线![]() 上,∴
上,∴![]() ,
,
∴![]()
∴点![]() 的轨迹是以
的轨迹是以![]() 为焦点,以4为长轴长的椭圆,
为焦点,以4为长轴长的椭圆,
∴![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,
∴曲线![]() 的方程为
的方程为![]() .
.
(2)∵直线![]() 与椭圆
与椭圆![]() 和抛物线
和抛物线![]() 都相切,∴直线
都相切,∴直线![]() 斜率一定存在,设
斜率一定存在,设![]() :
:![]() ①,
①,
①代入![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ②.
②.
有把①代入![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ③.
③.
由② ③解得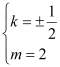
设![]() ,∵
,∵![]() 在第二象限,∴
在第二象限,∴![]() ,
,
注意![]() 与
与![]() 关于直线
关于直线![]() 对称,
对称,![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() :
:![]() ,
,
则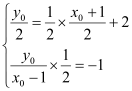 ,解得
,解得 ,经检验
,经检验![]() 在圆
在圆![]() 上,故所求点
上,故所求点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目

