题目内容
在平面直角坐标系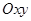 中,若双曲线
中,若双曲线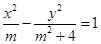 的焦距为8,则
的焦距为8,则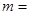
3
解析试题分析:通过双曲线的方程,判断实轴所在轴,求出c,利用焦距求出m的值即可. 解:因为在平面直角坐标系Oxy中,双曲线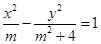 的焦距为8,所以m>0,焦点在x轴,所以a2=m,b2=m2+4,所以c2=m2+m+4,又双曲线
的焦距为8,所以m>0,焦点在x轴,所以a2=m,b2=m2+4,所以c2=m2+m+4,又双曲线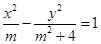 的焦距为8,所以:m2+m+4=16,即m2+m-12=0,解得m=3或m=-4(舍).故答案为:3.
的焦距为8,所以:m2+m+4=16,即m2+m-12=0,解得m=3或m=-4(舍).故答案为:3.
考点:双曲线的简单性质
点评:本题考查双曲线的简单性质的应用,判断双曲线的焦点所在的轴是解题的关键,法则容易出错.

练习册系列答案
相关题目
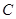 :
: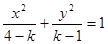 ,给出下面四个命题:
,给出下面四个命题: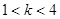 时,曲线
时,曲线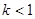 或
或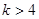 ;
;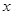 轴上的椭圆,则
轴上的椭圆,则 .
.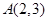 关于直线
关于直线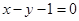 的对称点
的对称点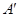 的坐标为 ;
的坐标为 ;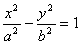
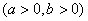 的渐近线与圆
的渐近线与圆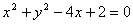 有公共点,则该双曲线的离心率的取值范围是___________.
有公共点,则该双曲线的离心率的取值范围是___________.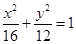 ,则以点
,则以点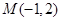 为中点的弦所在直线方程为__________________。
为中点的弦所在直线方程为__________________。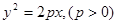 焦点的直线与抛物线交于
焦点的直线与抛物线交于 两点,
两点,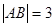 ,且
,且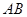 中点的纵坐标为
中点的纵坐标为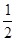 ,则
,则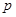 的值为______.
的值为______.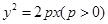 的焦点
的焦点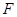 且斜率为
且斜率为 的直线与抛物线交于
的直线与抛物线交于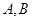 两点,且
两点,且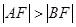 ,则
,则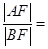 .
.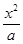 +
+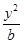 =1(
=1(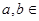 {1,2,3,4, ,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .
{1,2,3,4, ,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .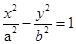 (a>0,b>0)的两个焦点。若在C上存在一点P。使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为________________.
(a>0,b>0)的两个焦点。若在C上存在一点P。使PF1⊥PF2,且∠PF1F2=30°,则C的离心率为________________.