[题目](1)设不等式2x-1＞m(x2-1)对满足|m|≤2的一切实数m的取值都成立.求x的取值范围,(2)是否存在m使得不等式2x-1＞m(x2-1)对满足|x|≤2的一切实数x的取值都成立．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】（1）设不等式2x－1＞m(x2－1)对满足|m|≤2的一切实数m的取值都成立，求x的取值范围；

（2）是否存在m使得不等式2x－1＞m(x2－1)对满足|x|≤2的一切实数x的取值都成立．

【答案】（1）（2）没有

【解析】试题分析：

（1）由题意构造变量为的函数，将问题转化为对恒成立的问题求解．（2）构造函数，问题即为当对恒成立时求的范围．然后分和两种情况，利用函数的图象，将问题化为不等式解决即可．

试题解析：

（1）设，

由题意得对恒成立，

∴，

解得．

∴实数x的取值范围为．

(2) 令，

由题意可得对恒成立．

①当时，则当时，f(x)= 2x－1，不满足题意．

②当时，若对恒成立，则需满足

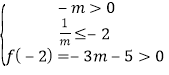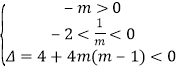或或，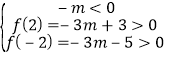

解不等式组可得，以上不等式组的解集均为空集．

所以不存在实数满足题意．

练习册系列答案

相关题目

【题目】（题文）如图在三棱锥中，分别为棱的中点，已知，

求证：（1）直线平面；

（2）平面平面.

【题目】已知函数，．

（）当时，证明：为偶函数；

（）若在上单调递增，求实数的取值范围；

（）若，求实数的取值范围，使在上恒成立．

【题目】为了选拔参加自行车比赛的选手，对自行车运动员甲、乙两人在相同条件下进行了6次测试，测得他们的最大速度(单位：m/s)的数据如下：

甲	27	38	30	37	35	31
乙	33	29	38	34	28	36

(1)画出茎叶图，由茎叶图你能获得哪些信息；

(2)估计甲、乙两运动员的最大速度的平均数和方差，并判断谁参加比赛更合适．

【题目】某单位需要从甲、乙人中选拔一人参加新岗位培训，特别组织了个专项的考试，成绩统计如下：

	第一项	第二项	第三项	第四项	第五项
甲的成绩
乙的成绩

（1）根据有关统计知识，回答问题:若从甲、乙人中选出人参加新岗培训，你认为选谁合适，请说明理由；

（2）根据有关槪率知识，解答以下问题：

从甲、乙人的成绩中各随机抽取一个，设抽到甲的成绩为，抽到乙的成绩为，用表示满足条件的事件，求事件的概率.

【题目】如图，在三棱柱中，底面，，，，是棱上一点．

（I）求证：．

（II）若，分别是，的中点，求证：平面．

（III）若二面角的大小为，求线段的长．

【题目】已知函数，其中a，b，c∈R．
（Ⅰ）若a=b=1，求函数f（x）的单调区间；
（Ⅱ）若a=0，且当x≥0时，f（x）≥1总成立，求实数b的取值范围；
（Ⅲ）若a＞0，b=0，若f（x）存在两个极值点x1 ， x2 ，求证；f（x1）+f（x2）＜e．

【题目】设x，y满足不等式组，若z=ax+y的最大值为2a+4，最小值为a+1，则实数a的取值范围为（）
A.[﹣1，2]
B.[﹣2，1]
C.[﹣3，﹣2]
D.[﹣3，1]

【题目】在极坐标系中，已知曲线C1的极坐标方程ρ2cos2θ=8，曲线C2的极坐标方程为θ= ，曲线C1 ， C2相交于A，B两点．以极点O为原点，极轴所在直线为x轴建立平面直角坐标系，已知直线l的参数方程为（t为参数）．
（1）求A，B两点的极坐标；
（2）曲线C1与直线l分别相交于M，N两点，求线段MN的长度．

试题分类