题目内容
【题目】已知椭圆![]() 右焦点
右焦点![]() ,离心率为
,离心率为![]() ,过
,过![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() ,设
,设![]() 中点分别为
中点分别为![]() .
.
(1)求椭圆的标准方程;
(2)证明:直线![]() 必过定点,并求出此定点坐标.
必过定点,并求出此定点坐标.

【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据题意确定出c与e的值,利用离心率公式求出a的值,进而求出b的值,确定出椭圆方程即可;
(2)由直线AB与CD向量存在,设为k,表示出AB方程,设出A与B坐标,进而表示出M坐标,联立直线AB与椭圆方程,消去y得到关于x的一元二次方程,利用根与系数的关系表示出M,同理表示出N,根据M与N横坐标相同求出k的值,得到此时MN斜率不存在,直线MN恒过定点;若直线MN斜率存在,表示出直线MN斜率,进而表示出直线MN,令y=0,求出x的值,得到直线MN恒过定点,综上,得到直线MN恒过定点,求出定点坐标即可;
解:(1) 由题意:![]() ,
,
∴![]() ,
,
则椭圆的方程为![]()
(2) ∵![]() 斜率均存在
斜率均存在
∴设直线![]() 方程为:
方程为:![]() ,
,
再设![]() ,则有
,则有![]() ,
,
联立得:![]() ,
,
消去![]() 得:
得:![]() ,
,
∴ ,即
,即![]() ,
,
将上式中的![]() 换成
换成![]() ,同理可得:
,同理可得:![]() ,
,
若![]() ,解得:
,解得:![]() ,直线
,直线![]() 斜率不存在,
斜率不存在,
此时直线![]() 过点
过点![]() ;
;
下证动直线![]() 过定点
过定点![]() ,
,
若直线![]() 斜率存在,则
斜率存在,则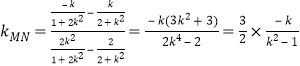 ,
,
直线![]() 为
为![]() ,
,
令![]() ,得
,得![]() ,
,
综上,直线![]() 过定点
过定点![]() ;
;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目