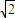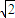题目内容
满足条件AB=2,AC=2BC的三角形ABC的面积最大值是
.
| 4 |
| 3 |
| 4 |
| 3 |
分析:设BC=x,根据面积公式用x和sinB表示出三角形的面积,再根据余弦定理用x表示出sinB,代入三角形的面积表达式,进而得到关于x的三角形面积表达式,再根据x的范围求得三角形面积的最大值.
解答:解:设BC=x,则AC=2x,由余弦定理可得 cosB=
=
.
由于三角形ABC的面积为
•2•x•sinB=x
=
=
=
.
再由三角形任意两边之和大于第三边可得
,解得
<x<2,故
<x2<4.
再利用二次函数的性质可得,当x2=
时,函数-9x4+40x2+16取得最大值为
,
故
的最大值为
,
故答案为
.
| x2+4-4x2 |
| 4x |
| 4-3x2 |
| 4x |
由于三角形ABC的面积为
| 1 |
| 2 |
| 1-cos2B |
x2[1-(
|
|
=
| ||
| 4 |
再由三角形任意两边之和大于第三边可得
|
| 2 |
| 3 |
| 4 |
| 9 |
再利用二次函数的性质可得,当x2=
| 20 |
| 9 |
| 256 |
| 9 |
故
| ||
| 4 |
| 4 |
| 3 |
故答案为
| 4 |
| 3 |
点评:本题主要考查了余弦定理和面积公式在解三角形中的应用.当涉及最值问题时,可考虑用函数的单调性和定义域等问题,属于中档题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
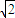
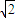 <R+r
<R+r