题目内容
正方形ABCD中,AB=1,分别以A、C为圆心作两个半径为R、r(R>r)的圆,当R、r满足条件11时,⊙A与⊙C有2个交点.( )A.R+r>
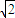
B.R-r<
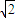 <R+r
<R+rC.R-r>
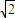
D.0<R-r<
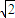
【答案】分析:根据题意并且结合勾股定理可得两圆的圆心距AC=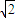 ,由⊙A与⊙C有2个交点,可得圆心距大于两圆半径之差,并且小于两圆半径之和,进而得到答案.
,由⊙A与⊙C有2个交点,可得圆心距大于两圆半径之差,并且小于两圆半径之和,进而得到答案.
解答:解:因为正方形ABCD中,AB=1,
所以由勾股定理可得两圆的圆心距AC=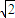 ,
,
因为⊙A与⊙C有2个交点,即两圆相交,
所以圆心距大于两圆半径之差,并且小于两圆半径之和,
因为R>r,
所以R-r<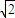 <R+r.
<R+r.
故选B.
点评:本题注意考查两个圆的位置关系与圆心钜之间的关系,以及勾股定理,此题属于基础题.
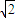 ,由⊙A与⊙C有2个交点,可得圆心距大于两圆半径之差,并且小于两圆半径之和,进而得到答案.
,由⊙A与⊙C有2个交点,可得圆心距大于两圆半径之差,并且小于两圆半径之和,进而得到答案.解答:解:因为正方形ABCD中,AB=1,
所以由勾股定理可得两圆的圆心距AC=
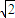 ,
,因为⊙A与⊙C有2个交点,即两圆相交,
所以圆心距大于两圆半径之差,并且小于两圆半径之和,
因为R>r,
所以R-r<
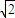 <R+r.
<R+r.故选B.
点评:本题注意考查两个圆的位置关系与圆心钜之间的关系,以及勾股定理,此题属于基础题.

练习册系列答案
相关题目
 如图,边长为4的正方形ABCD中
如图,边长为4的正方形ABCD中