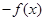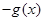题目内容
曲线f(x)=x㏑x在点x=1处的切线方程是( )
| A.y=2x+2 | B.y=2x-2 | C.y=x-1 | D.y=x+1 |
C
解析试题分析:根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成一般式即可解:y="xlnx," y'=1×lnx+x•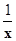 ="1+lnx," y'(1)=1又当x=1时y=0,∴切线方程为y="x-1" 即x-y-1=0,故选:C
="1+lnx," y'(1)=1又当x=1时y=0,∴切线方程为y="x-1" 即x-y-1=0,故选:C
考点:导数的几何意义
点评:此题主要考查导数的计算,以及利用导数研究曲线上某点切线方程,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
函数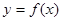 在一点的导数值为
在一点的导数值为 是函数
是函数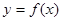 在这点取极值的( )
在这点取极值的( )
| A.充分条件 | B.必要条件 | C.必要非充分条件 | D.充要条件 |
曲线 上的点到直线
上的点到直线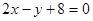 的最短距离是( )
的最短距离是( )
A.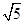 | B. | C.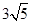 | D.0 |
已知函数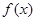 在
在 上连续可导,则
上连续可导,则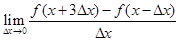 等于 ( )
等于 ( )
A.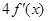 | B.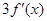 | C.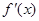 | D.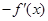 |
曲线 在
在 处的切线平行于直线
处的切线平行于直线 ,则
,则 点的坐标为( )
点的坐标为( )
A.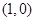 | B. |
C.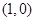 和 和 | D. 和 和 |
函数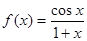 在
在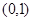 处的切线方程是
处的切线方程是
A.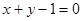 | B.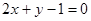 | C.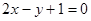 | D.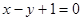 |
设 为曲线
为曲线 :
: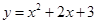 上的点,且曲线
上的点,且曲线 在点
在点 处切线倾斜角的取值范围为
处切线倾斜角的取值范围为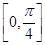 ,则点
,则点 横坐标的取值范围为 ( )
横坐标的取值范围为 ( )
A.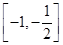 | B.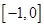 | C.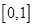 | D.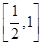 |
如右图,阴影部分的面积是 ( )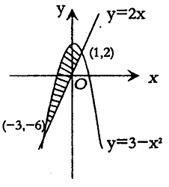
A.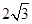 | B.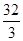 | C.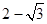 | D.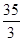 |
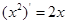 ,
,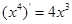 ,
,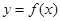 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在 上的函数
上的函数 满足
满足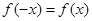 ,记
,记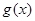 为
为 =( )
=( )