题目内容
函数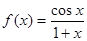 在
在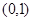 处的切线方程是
处的切线方程是
A.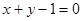 | B.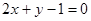 | C.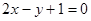 | D.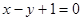 |
A
解析试题分析:∵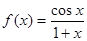 ,∴
,∴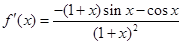 ,∴在
,∴在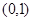 处的切线斜率k=
处的切线斜率k= ,∴在
,∴在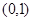 处的切线方程为y-1=-1(x-0)即
处的切线方程为y-1=-1(x-0)即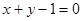 ,故选A
,故选A
考点:本题考查了导数的几何意义
点评: 在
在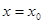 处导数
处导数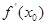 即为
即为 所表示曲线在
所表示曲线在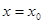 处切线的斜率,即
处切线的斜率,即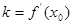 ,则切线方程为:
,则切线方程为: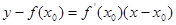

练习册系列答案
相关题目
已知函数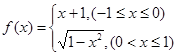 , 则
, 则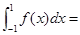 ( )
( )
A. | B.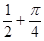 | C.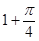 | D.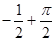 |
已知可导函数 的导函数为
的导函数为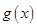 ,且满足:①
,且满足:①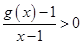 ,②
,②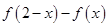
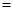
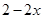 ,记
,记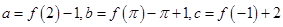 ,则
,则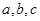 的大小顺序为( )
的大小顺序为( )
A.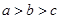 | B.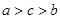 | C.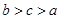 | D.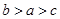 |
曲线f(x)=x㏑x在点x=1处的切线方程是( )
| A.y=2x+2 | B.y=2x-2 | C.y=x-1 | D.y=x+1 |
函数 在点
在点 处的导数是
处的导数是
A. | B. | C. | D. |
若函数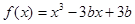 在
在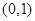 内有极小值,则 ( )
内有极小值,则 ( )
A.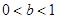 | B.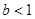 | C.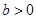 | D.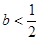 |
函数 在
在 上是增函数,则实数
上是增函数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
从如图所示的正方形OABC区域内任取一个点 ,则点M取自阴影部分的概率为
,则点M取自阴影部分的概率为 
A. | B. | C. | D. |
已知 为一次函数,且
为一次函数,且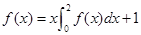 ,则
,则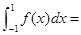 ( )
( )
A.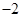 | B.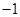 | C.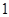 | D.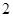 |