题目内容
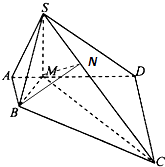
【题目】如图，几何体EF﹣ABCD中，CDEF为边长为2的正方形，ABCD为直角梯形，AB∥CD，AD⊥DC，AD=2，AB=4，∠ADF=90°．
（Ⅰ）求证：AC⊥FB
（Ⅱ）求二面角E﹣FB﹣C的大小．
【答案】（Ⅰ）见解析；（Ⅱ） 
.
【解析】试题分析：
(Ⅰ)由题意结合线面垂直的判定定理可证得AC⊥平面FCB，据此有AC⊥FB．
(Ⅱ)建立空间直角坐标系，结合半平面的法向量可得二面角E﹣FB﹣C的大小为
.
试题解析：
（Ⅰ）证明：由题意得，AD⊥DC，AD⊥DF，且DC∩DF=D，
∴AD⊥平面CDEF，∴AD⊥FC，
∵四边形CDEF为正方形．∴DC⊥FC
由DC∩AD=D ∴FC⊥平面ABCD，∴FC⊥AC
又∵四边形ABCD为直角梯形，
AB∥CD，AD⊥DC，AD=2，AB=4
∴
， 
，则有AC2+BC2=AB2∴AC⊥BC
由BC∩FC=C，∴AC⊥平面FCB，∴AC⊥FB．
（Ⅱ）解：由（I）知AD，DC，DE所在直线相互垂直，故以D为原点，以
的方向分别为x，y，z轴的正方向，建立如图所示的空间直角坐标系D-xyz…
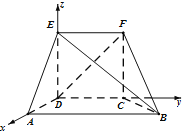
可得D（0，0，0），F（0，2，2），B（2，4，0），
E（0，0，2），C（0，2，0），A（2，0，0），
由（Ⅰ）知平面FCB的法向量为
∵
， 
…
设平面EFB的法向量为
则有
即
令
则
设二面角E﹣FB﹣C的大小为θ，有图易知
为锐角
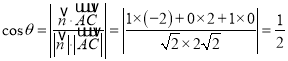
所以二面角E﹣FB﹣C的大小为
…
练习册系列答案
相关题目
