题目内容
定义在R上的偶函数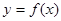 ,满足
,满足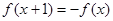 ,且在
,且在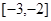 上是减函数,若
上是减函数,若 ,
,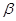 是锐角三角形的两个内角,则 ( )
是锐角三角形的两个内角,则 ( )
A.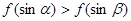 B.
B.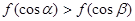
C.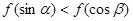 D.
D.
【答案】
D
【解析】本试题主要是考查了抽象函数的奇偶性和单调性和三角不等式的综合运用
∵f(x+1)=-f(x),∴f(x+2)=-f(x+1)=f(x),f(x)是周期为2的周期函数.
∵y=f(x)是定义在R上的偶函数,∴f(-x)=f(x),∵f(x)在[-3,-2]上是减函数,
∴在[2,3]上是增函数,∴在[0,1]上是增函数,∵α,β是锐角三角形的两个内角.
∴α+β>90°,α>90°-β,两边同取正弦得:sinα>sin(90°-β)=cosβ,且sinα、cosβ都在区间[0,1]上,∴f(sinα)>f(cosβ),故答案选 D.
解决该试题的关键是理解1>sinα>cosβ>0,结合单调性判定。

练习册系列答案
相关题目
定义在R上的偶函数满足:对任意x1,x2∈[0,+∞),且x1≠x2都有
>0,则( )
| f(x1)-f(x2) |
| x1-x2 |
| A、f(3)<f(-2)<f(1) |
| B、f(1)<f(-2)<f(3) |
| C、f(-2)<f(1)<f(3) |
| D、f(3)<f(1)<f(-2) |