题目内容
设等差数列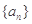 的前n项和为Sn,若a1=-15,
a3+a5= -18,则当Sn取最小值时n等于( )
的前n项和为Sn,若a1=-15,
a3+a5= -18,则当Sn取最小值时n等于( )
A.9 B.8 C.7 D.6
【答案】
B
【解析】
试题分析:根据等差数列的性质化简a3+a5=-18,得到a4的值,然后根据a1的值,利用等差数列的通项公式即可求出公差d的值,根据a1和d的值写出等差数列的通项公式,进而写出等差数列的前n项和公式Sn,配方后即可得到Sn取最小值时n的值.解:由等差数列的性质可得 a3+a5=2a4=-18,解得a4=-9. 又a1=-15,设公差为d,所以,a4=a1+3d=-15+3d=-9,解得d="2" .则an=-15+2(n-1)=2n-17,那么可知所以a8<0, a9>0,当n=8时,Sn取最小值.故选B.
考点:等差数列的通项公式及前n项和公式
点评:此题考查学生灵活运用等差数列的通项公式及前n项和公式化简求值,掌握等差数列的性质,是一道中档题.

练习册系列答案
相关题目
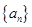 的前n项和为
的前n项和为 ,若
,若 ,
, ,则当
,则当 的前n项和为
的前n项和为 ,且
,且 (c是常数,
(c是常数,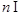 N*),
N*), .
. .
.