题目内容
设等差数列的前n项和为Sn，若S3=9，S6=36，则a8=
15
15
．分析：由S6-S3=a4+a5+a6，利用等差数列的通项公式及性质化简，求出公差d的值，进而求出首项a1的值，然后利用等差数列的通项公式化简a8后，将d与a1的值代入，即可求出a8的值．
解答：解：∵S3=9，S6=36，
∴a4+a5+a6=S6-S3=36-9=27，
又a4+a5+a6=（a1+3d）+（a2+3d）+（a3+3d）=（a1+a2+a3）+9d=S3+9d=9+9d=27，
∴d=2，
∵a4+a5+a6=3a5=27，
∴a5=a1+4d=a1+8=9，即a1=1，
则a8=a1+7d=1+14=15．
故答案为：15
∴a4+a5+a6=S6-S3=36-9=27，
又a4+a5+a6=（a1+3d）+（a2+3d）+（a3+3d）=（a1+a2+a3）+9d=S3+9d=9+9d=27，
∴d=2，
∵a4+a5+a6=3a5=27，
∴a5=a1+4d=a1+8=9，即a1=1，
则a8=a1+7d=1+14=15．
故答案为：15
点评：此题考查了等差数列的性质，以及等差数列的通项公式，熟练掌握性质及公式是解本题的关键．
练习册系列答案
相关题目
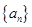的前n项和为
,若
,
,则当
的前n项和为
,若
,
,则当
的前n项和为
，且
（c是常数，
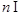N*），
.
.