题目内容
【题目】如图,在直角梯形![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的高.
的高.

【答案】(1)见解析(2)1
【解析】分析:(1)由题意可得BD⊥CD,再利用面面垂直的性质即可证明CD⊥平面ABD;
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,利用等体积法即可求得三棱锥
,利用等体积法即可求得三棱锥![]() 的高.
的高.
详解:(1)证明:∵AB=AD,AB⊥AD,∴∠ADB=45°,
又∵AD∥BC,∠DBC=45°,
又∵∠BCD=45°,∴BD⊥CD;
又∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴CD⊥平面ABD.
(2)方法一:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
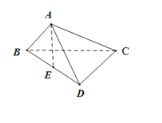
∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]()
又∵平面![]() ⊥平面
⊥平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]()
∴![]()
由(1)知![]()
所以![]()
![]()
设棱锥![]() 的高为
的高为![]()
![]()
![]()
![]()
方法二:由(1)知CD⊥平面ABD,所以CD⊥AB.
又因为AB⊥AD,![]()
所以AB⊥平面ACD
所以棱锥![]() 的高为
的高为![]()

 阶梯计算系列答案
阶梯计算系列答案【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
(1)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,由以上数据完成下列2×2列联表,并判断能否在犯错误的概率不超过0.005的前提下,认为“移动支付活跃用户”与性别有关?
移动支付活跃用户 | 非移动支付活跃用户 | 总计 | |
男 | |||
女 | |||
总计 | 100 |
(2)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户.为了鼓励男性用户使用移动支付,对抽出的男“移动支付达人”每人奖励300元,记奖励总金额为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附公式及表如下:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】红铃虫是棉花的主要害虫之一,也侵害木棉、锦葵等植物.为了防治虫害,从根源上抑制害虫数量.现研究红铃虫的产卵数和温度的关系,收集到7组温度![]() 和产卵数
和产卵数![]() 的观测数据于表I中.根据绘制的散点图决定从回归模型①
的观测数据于表I中.根据绘制的散点图决定从回归模型①![]() 与回归模型②
与回归模型②![]() 中选择一个来进行拟合.
中选择一个来进行拟合.
表I
温度 | 20 | 22 | 25 | 27 | 29 | 31 | 35 |
产卵数 | 7 | 11 | 21 | 24 | 65 | 114 | 325 |
(1)请借助表II中的数据,求出回归模型①的方程:
表II(注:表中![]() )
)
|
|
|
|
|
|
|
|
|
189 | 567 | 25.27 | 162 | 78106 | 11.06 | 3040 | 41.86 | 825.09 |
(2)类似的,可以得到回归模型②的方程为![]() .试求两种模型下温度为
.试求两种模型下温度为![]() 时的残差;
时的残差;
(3)若求得回归模型①的相关指数![]() ,回归模型②的相关指数
,回归模型②的相关指数![]() ,请结合②说明哪个模型的拟合效果更好.
,请结合②说明哪个模型的拟合效果更好.
参考数据:![]()
附:回归方程![]() 中
中 相关指数
相关指数
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过![]() 的前提下认为喜好体育运动与性别有关?说明你的理由.
的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式: ![]() )
)
临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |