题目内容
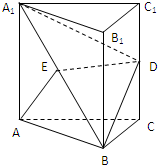 如图,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分别为CC1、A1B的中点.
如图,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分别为CC1、A1B的中点.(1)求证:DE∥平面ABC;
(Ⅱ)求证:AE⊥BD;
(Ⅲ)求三棱锥D-A1BA的体积.
分析:(Ⅰ)利用三角形的中位线定理、平行四边形的判定定理和性质定理及线面平行的判定定理即可得出;
(Ⅱ)利用线面垂直的判定定理和性质定理即可证明;
(Ⅲ)利用三棱锥的体积计算公式即可得出.
(Ⅱ)利用线面垂直的判定定理和性质定理即可证明;
(Ⅲ)利用三棱锥的体积计算公式即可得出.
解答:证明:(Ⅰ)如图所示:取AB的中点F,连接EF、CF、ED.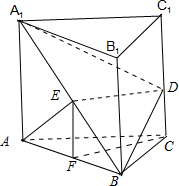
又∵BE=EA1,∴EF
AA1.
由已知得CD
AA1,∴CD
EF.
∴四边形EFCD为平行四边形,
∴ED∥FC.
又∵ED?平面ABC,CF?平面ABC.
∴ED∥平面ABC.
(Ⅱ)由正三棱柱ABC-A1B1C1,可得A1A⊥底面ABC,∴A1A⊥CF.
由F是正△ABC的边AB的中点,∴CF⊥AB.
又A1A∩AB=A,∴CF⊥侧面ABB1A1,
∵ED∥FC,∴DE⊥侧面ABB1A1.
∴DE⊥AE.
在等腰△ABA1中,由AB=AA1,BE=EA1.
∴AE⊥A1B.
又∵A1B∩DE=E.
∴AE⊥平面A1BD.
∴AE⊥BD.
(Ⅲ)由(Ⅱ)可知:DE⊥侧面ABB1A1,且DE=CF=
a.
∴V三棱锥D-ABA1=
×S△ABA1×DE=
×
(2a)2×
a=
.

又∵BE=EA1,∴EF
| ∥ |
. |
| 1 |
| 2 |
由已知得CD
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴四边形EFCD为平行四边形,
∴ED∥FC.
又∵ED?平面ABC,CF?平面ABC.
∴ED∥平面ABC.
(Ⅱ)由正三棱柱ABC-A1B1C1,可得A1A⊥底面ABC,∴A1A⊥CF.
由F是正△ABC的边AB的中点,∴CF⊥AB.
又A1A∩AB=A,∴CF⊥侧面ABB1A1,
∵ED∥FC,∴DE⊥侧面ABB1A1.
∴DE⊥AE.
在等腰△ABA1中,由AB=AA1,BE=EA1.
∴AE⊥A1B.
又∵A1B∩DE=E.
∴AE⊥平面A1BD.
∴AE⊥BD.
(Ⅲ)由(Ⅱ)可知:DE⊥侧面ABB1A1,且DE=CF=
| 3 |
∴V三棱锥D-ABA1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
点评:熟练掌握线面平行、垂直的判定定理和性质定理及三棱锥的体积计算公式是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点.
如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为线段A1B上的动点. 如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为2cm,高位5cm,一质点自A点出发,沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1,D是AC的中点,
如图,已知正三棱柱ABC-A1B1C1,D是AC的中点, (2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为
(2011•重庆三模)如图,已知正三棱柱ABC-A1B1C1的所有棱长均为a,截面AB1C和A1BC1相交于DE,则三棱锥B-B1DE的体积为