题目内容
给出下列四个命题,其中正确命题序号是 .
①若b2=ac,则b是a,c的等比中项.
②数列{an}既是等差数列,又是等比数列,则{an}是常数列.
③若数列{an}的前n项和Sn=2×3n-2,则{an}是等比数列.
④若a,b,c成等比数列,则lga,lgb,lgc成等差数列.
①若b2=ac,则b是a,c的等比中项.
②数列{an}既是等差数列,又是等比数列,则{an}是常数列.
③若数列{an}的前n项和Sn=2×3n-2,则{an}是等比数列.
④若a,b,c成等比数列,则lga,lgb,lgc成等差数列.
分析:逐个验证:①举反例a=b=c=0;④举反例a=-1,b=-2,c=-4,②设等差数列{an}的公差为d,又{an}为等比数列,故(a1+d)2=a1(a1+2d),解得d=0,可得数列为常数列;③由an与Sn的关系可得an=4×3n-1,由等比数列的定义可得.
解答:解:逐个验证:①取a=b=c=0,显然满足b2=ac,但不满足b是a,c的等比中项,故错误;
②设等差数列{an}的公差为d,又{an}为等比数列,故(a1+d)2=a1(a1+2d),解得d=0,故{an}是常数列,正确;
③当n≥2时,an=Sn-Sn-1=(2×3n-2)-(2×3n-1-2)=4×3n-1,当n=1时,a1=S1=2×31-2=4,显然也满足,
故an=4×3n-1,满足
=
=3,故{an}是等比数列,正确;
④不妨取a=-1,b=-2,c=-4,显然满足a,b,c成等比数列,不满足lga,lgb,lgc成等差数列,故错误.
故答案为:②③
②设等差数列{an}的公差为d,又{an}为等比数列,故(a1+d)2=a1(a1+2d),解得d=0,故{an}是常数列,正确;
③当n≥2时,an=Sn-Sn-1=(2×3n-2)-(2×3n-1-2)=4×3n-1,当n=1时,a1=S1=2×31-2=4,显然也满足,
故an=4×3n-1,满足
| an+1 |
| an |
| 4×3n |
| 4×3n-1 |
④不妨取a=-1,b=-2,c=-4,显然满足a,b,c成等比数列,不满足lga,lgb,lgc成等差数列,故错误.
故答案为:②③
点评:本题考查等差数列和等比数列的性质,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


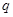 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与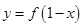 图像关于
图像关于 对称.
对称.