题目内容
已知x,y满足约束条件
(1)求目标函数z=2x-y的最大值和最小值;
(2)若目标函数z=ax+y取得最大值的最优解有无穷多个,求a的值;
(3)求z=x2+y2的取值范围.

(1)求目标函数z=2x-y的最大值和最小值;
(2)若目标函数z=ax+y取得最大值的最优解有无穷多个,求a的值;
(3)求z=x2+y2的取值范围.
(1)zmax=2×5-3=7,zmin=2×1- =-
=- .
.
(2)a= .
.
(3)[ ,34]
,34]
 =-
=- .
.(2)a=
 .
.(3)[
 ,34]
,34]解:(1)作出不等式组表示的可行域如图:

作直线l:2x-y=0,并平行移动使它过可行域内的B点,此时z有最大值;过可行域内的C点,此时z有最小值,
解 ,得A(1,
,得A(1, ).
).
解 ,得B(5,3).
,得B(5,3).
解 ,得C(1,
,得C(1, ).
).
∴zmax=2×5-3=7,zmin=2×1- =-
=- .
.
(2)一般情况下,当z取得最大值时,直线所经过的点都是唯一的,但若直线平行于边界直线,即直线z=ax+y平行于直线3x+5y=30时,线段BC上的任意一点均使z取得最大值,此时满足条件的点即最优解,有无数个.
又kBC=- ,∴-a=-
,∴-a=- ,∴a=
,∴a= .
.
(3)z=x2+y2,则 为(x,y)与原点(0,0)的距离,结合不等式的区域,易知A点到原点距离最小为
为(x,y)与原点(0,0)的距离,结合不等式的区域,易知A点到原点距离最小为 ,最大值为|OB|、|OC|、原点O到直线3x+5y=30距离三者之一,计算得,最大值为|OB|=
,最大值为|OB|、|OC|、原点O到直线3x+5y=30距离三者之一,计算得,最大值为|OB|=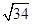 .故z=x2+y2的取值范围是[
.故z=x2+y2的取值范围是[ ,34].
,34].

作直线l:2x-y=0,并平行移动使它过可行域内的B点,此时z有最大值;过可行域内的C点,此时z有最小值,
解
 ,得A(1,
,得A(1, ).
).解
 ,得B(5,3).
,得B(5,3).解
 ,得C(1,
,得C(1, ).
).∴zmax=2×5-3=7,zmin=2×1-
 =-
=- .
.(2)一般情况下,当z取得最大值时,直线所经过的点都是唯一的,但若直线平行于边界直线,即直线z=ax+y平行于直线3x+5y=30时,线段BC上的任意一点均使z取得最大值,此时满足条件的点即最优解,有无数个.
又kBC=-
 ,∴-a=-
,∴-a=- ,∴a=
,∴a= .
.(3)z=x2+y2,则
 为(x,y)与原点(0,0)的距离,结合不等式的区域,易知A点到原点距离最小为
为(x,y)与原点(0,0)的距离,结合不等式的区域,易知A点到原点距离最小为 ,最大值为|OB|、|OC|、原点O到直线3x+5y=30距离三者之一,计算得,最大值为|OB|=
,最大值为|OB|、|OC|、原点O到直线3x+5y=30距离三者之一,计算得,最大值为|OB|=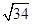 .故z=x2+y2的取值范围是[
.故z=x2+y2的取值范围是[ ,34].
,34].
练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
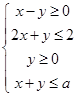 ,表示的平面区域是一个三角形区域,则
,表示的平面区域是一个三角形区域,则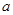 的取值范围是( )
的取值范围是( )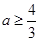
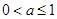
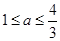
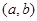 在直线
在直线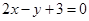 的右下方,则( )
的右下方,则( )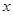 、
、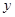 满足约束条件
满足约束条件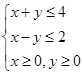 ,则
,则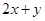 的最大值是( )
的最大值是( )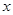 、
、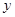 满足
满足 ,且
,且 的最小值为
的最小值为 ,则
,则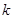 的值为( )
的值为( )

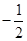
 ,若目标函数z=ax+y(a≠0)取得最小值时的最优解有无数个,则实数a的值为________.
,若目标函数z=ax+y(a≠0)取得最小值时的最优解有无数个,则实数a的值为________.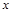
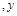 满足
满足 则
则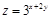 的最小值是 .
的最小值是 . 、
、 满足约束条件
满足约束条件 ,则
,则 的取值范围是( )
的取值范围是( )



 ,则目标函数z="2x" +y的最大值是( ).
,则目标函数z="2x" +y的最大值是( ).