��Ŀ����
����Ŀ��ijѧУ�о���ѧϰС��Ը�У�߶�ѧ������������е��飬ѧϰС���Ա���֣�ѧϰ�ɼ�ͻ����ѧ�������ӵıȽ϶࣬Ϊ���о�ѧ����������ѧϰ�ɼ��Ƿ��й�ϵ�����꼶������1��50����951��1000����ѧ�������˵��飬�õ��������ݣ�
�꼶���� �Ƿ���� | 1��50 | 951��1000 |
���� | 41 | 32 |
������ | 9 | 18 |
��1�����ݱ��е����ݣ��ܷ��ڷ����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��
��2���ڣ�1���е����100��ѧ���У����շֲ�����ڲ����ӵ�ѧ���г�ȡ��9�ˣ���һ�������������õĻ���ϰ�ߣ���������9������ȡ3�ˣ���������1��50����ѧ������Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
����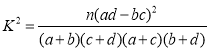
���𰸡���1���ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ��2������������ѧ����1
��������
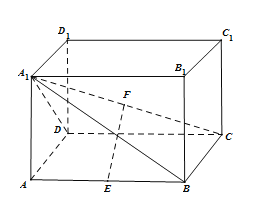
��1���������ݴ���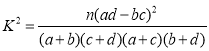 ���ý�.
���ý�.
��2��![]() ���ӳ����ηֲ������ø��ʹ�ʽ�ɵý�.
���ӳ����ηֲ������ø��ʹ�ʽ�ɵý�.
�⣺��1��![]()
����ڷ�����ĸ��ʲ�����0.05��ǰ������Ϊ������ѧϰ�ɼ��й�ϵ
��2����������9�����꼶������![]() ����
����![]() ���ֱ���3�˺�6��.
���ֱ���3�˺�6��.
![]() ��ȡ0��1��2��3
��ȡ0��1��2��3
![]()
![]()
![]()
![]()
![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 | |
|
|
|
|
|
��ѧ�ɼ� |
|
|
|
|
|
�����ɼ� |
|
|
|
|
|
��1�����ݱ���![]() ��
��![]() ֮���н�ǿ�����Թ�ϵ����
֮���н�ǿ�����Թ�ϵ����![]() ��
��![]() �����Իع鷽�̣�
�����Իع鷽�̣�
��2�����ο����У��涨��ѧ�ɼ��ﵽ![]() ��Ϊ���㣬�����ɼ��ﵽ
��Ϊ���㣬�����ɼ��ﵽ![]() ��Ϊ����.���ð���ѧ�����������������ʷֱ�Ϊ
��Ϊ����.���ð���ѧ�����������������ʷֱ�Ϊ![]() ��
��![]() ���ҳ�ȥ���ߵ�
���ҳ�ȥ���ߵ�![]() ��ͬѧ�⣬ʣ�µ�ͬѧ����ѧ���㵫�����������ͬѧ����
��ͬѧ�⣬ʣ�µ�ͬѧ����ѧ���㵫�����������ͬѧ����![]() �ˣ���д��
�ˣ���д��![]() ���������ж��ܷ��ڷ�����ĸ��ʲ�����
���������ж��ܷ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ��ѧ���������������йأ�
��ǰ������Ϊ��ѧ���������������йأ�
�ο����ݣ�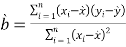 ��
��![]() ��
��![]() ��
��![]() ��
��![]()