��Ŀ����
19����֪����{an}��ǰn��Ϊ��Sn������Sn=$\frac{1}{2}$n2+$\frac{11}{2}$n������{bn}����bn+2-2bn+1+bn=0��n��N*������b3=11��ǰ9���Ϊ153����1��������{an}��{bn}��ͨ�ʽ��
��2����cn=$\frac{3}{��2{a}_{n}-11����2{b}_{n}-1��}$������{cn}��ǰn���ΪTn����ʹ�ò���ʽTn��$\frac{k}{25}$��һ��n��N*�����������������k��ֵ��
���� ��1��ͨ��an=Sn-Sn-1�ɵ�an=n+5����֤��n=1ʱ�������ɣ�ͨ��bn+2-2bn+1+bn=0��n��N*�����ɵ�����{bn}Ϊ�Ȳ����У����乫��Ϊd������S9=9b5=9��b3+2d�����㼴�ɣ�
��2��ͨ��an=n+5��bn=3n+2�������ĸ�ɵ�cn=$\frac{1}{2}$��$\frac{1}{2n-1}$-$\frac{1}{2n+1}$����������ӿɵ�Tn=$\frac{1}{2}$��1-$\frac{1}{2n+1}$������$\frac{1}{2}$��1-$\frac{1}{2n+1}$����$\frac{k}{25}$��һ��n��N*�����������㼴�ɣ�
��� �⣺��1����Sn=$\frac{1}{2}$n2+$\frac{11}{2}$n��
��an=Sn-Sn-1=$\frac{1}{2}$n2+$\frac{11}{2}$n-$\frac{1}{2}$��n-1��2-$\frac{11}{2}$��n-1��=n+5��
�֡�a1=S1=$\frac{1}{2}+\frac{11}{2}$=6����Ҫ��
������{an}��ͨ��an=n+5��
��bn+2-2bn+1+bn=0��n��N*����
������{bn}Ϊ�Ȳ����У����乫��Ϊd��
�֡�b3=11��ǰ9���Ϊ153��
��153=9b5=9��b3+2d��=9��11+2d����
������d=3��
��b1=b3-2d=11-2��3=5��
������{bn}��ͨ��bn=5+3��n-1��=3n+2��
��2����an=n+5��bn=3n+2��
��cn=$\frac{3}{��2{a}_{n}-11����2{b}_{n}-1��}$=$\frac{3}{��2n+10-11����6n+4-1��}$=$\frac{1}{��2n-1����2n+1��}$=$\frac{1}{2}$��$\frac{1}{2n-1}$-$\frac{1}{2n+1}$����
��Tn=$\frac{1}{2}$��1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+��+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$��
=$\frac{1}{2}$��1-$\frac{1}{2n+1}$����
���ʽTn��$\frac{k}{25}$��һ��n��N*�������ȼ���$\frac{1}{2}$��1-$\frac{1}{2n+1}$����$\frac{k}{25}$��һ��n��N*��������
��$\frac{n}{2n+1}$$��\frac{k}{25}$����k��$\frac{25n}{2n+1}$=$\frac{25}{2+\frac{1}{n}}$��$\frac{25}{3}$��
�����������k��ֵΪ8��
���� ������һ�������벻��ʽ���ۺ��⣬�������е�ͨ���ͣ������������������ע����ⷽ���Ļ��ۣ������е��⣮

| A�� | 0040 | B�� | 0795 | C�� | 0815 | D�� | 0420 |
| A�� | $��x-1+\sqrt{3}i����x-1-\sqrt{3}i��$ | B�� | $��\sqrt{2}x-\sqrt{2}+\sqrt{3}i����\sqrt{2}x-\sqrt{2}-\sqrt{3}i��$ | C�� | 2��x-1+i����x-1-i�� | D�� | 2��x+1+i����x+1-i�� |

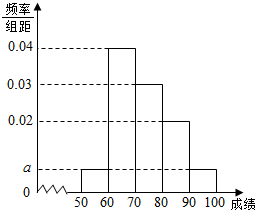 ijУ100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]��
ijУ100��ѧ�����п������ijɼ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ�����гɼ����������ǣ�[50��60����[60��70����[70��80����[80��90����[90��100]��