题目内容
(本小题满分15分)
等比数列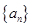 的各项均为正数,且
的各项均为正数,且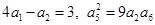 . (1)求数列
. (1)求数列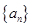 的通项公式;
的通项公式;
(2)设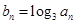 ,求数列
,求数列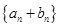 的前
的前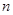 项和
项和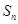 .
.
等比数列
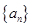 的各项均为正数,且
的各项均为正数,且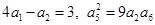 . (1)求数列
. (1)求数列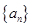 的通项公式;
的通项公式;(2)设
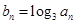 ,求数列
,求数列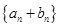 的前
的前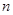 项和
项和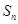 .
.( 1) (2)bn=n, Sn=
(2)bn=n, Sn=
 (2)bn=n, Sn=
(2)bn=n, Sn=
试题分析:(1)因为
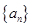 的各项均为正数,
的各项均为正数,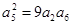 ,所以
,所以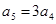 ,即q=3.
,即q=3.又
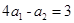 ,所以
,所以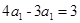 ,即
,即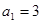 ,
,所以
 …………7分
…………7分(2)
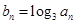 =n,所以
=n,所以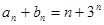 ,所以
,所以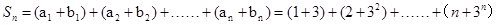
=
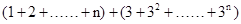 =
= 。…………15分
。…………15分点评:求等差数列和等比数列的通项公式及求数列的前n项和是数列的最基础的考查,是高考中的基础试题,对考生的要求是熟练掌握公式,并能进行一些基本量之间的运算。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, ,单调增数列
,单调增数列 的前
的前 项和为
项和为 ,
, ,且
,且 (
( ).
). (
( 的所有
的所有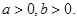 若
若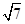 是
是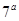 与
与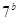 的等比中项,则
的等比中项,则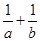 的最小值为
的最小值为 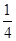
 满足
满足 和
和 ,则
,则
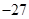
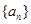 中,
中,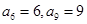 那么
那么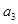 为 ( )
为 ( )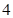
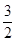
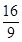
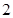
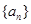 的公比
的公比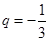 ,则
,则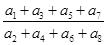 等于( )
等于( )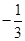
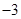
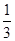
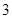
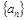 的前n项和为Sn,若S10=2,S30=14,则S20等于
的前n项和为Sn,若S10=2,S30=14,则S20等于 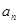 }中,
}中,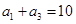 ,
,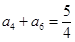 ,则等比数列{
,则等比数列{