题目内容
棱长都相等的四面体A-BCD的截EFGH平行于对棱AC、BD，则截面EFGH为
矩形
矩形
．分析：根据平行线的性质证明四边形EFGH是矩形．
解答：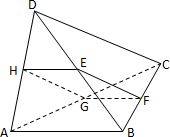
解：∵CD∥面EFGH，CD?平面BCD，
而平面EFGH∩平面BCD=EF．∴CD∥EF同理HG∥CD．∴EF∥HG
同理HE∥GF．∴四边形EFGH为平行四边形
由CD∥EF，HE∥AB
∴∠HEF（或其补角）为CD和AB所成的角，
又∵CD⊥AB．∴HE⊥EF．∴四边形EFGH为矩形．
故答案为 矩形
解：∵CD∥面EFGH，CD?平面BCD，而平面EFGH∩平面BCD=EF．∴CD∥EF同理HG∥CD．∴EF∥HG
同理HE∥GF．∴四边形EFGH为平行四边形
由CD∥EF，HE∥AB
∴∠HEF（或其补角）为CD和AB所成的角，
又∵CD⊥AB．∴HE⊥EF．∴四边形EFGH为矩形．
故答案为 矩形
点评：本题主要考查空间直线和平面位置关系的判断和应用，考查学生的运算和推理能力．
练习册系列答案
名校课堂系列答案
相关题目
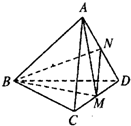8、棱长都相等的四面体称为正四面体．在正四面体A-BCD中，点M，N分别是CD和AD的中点，
