题目内容
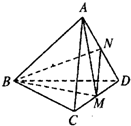 8、棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,
8、棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,给出下列命题:
①直线MN∥平面ABC;
②直线CD⊥平面BMN;
③三棱锥B-AMN的体积是三棱锥B-ACM的体积的一半.
则其中正确命题的序号为
①③
.分析:由点M,N分别是CD和AD的中点,结合三角形中位线定理及线面平等的判定定理我们可以判断①的对错,然后再由线面垂直的判定及性质可以判断②的真假;再由棱锥体积公式,分析两个三棱锥的高与底面积之间的关系,判断出③的正误,即可得到答案.
解答:解:∵点M,N分别是CD和AD的中点,
∴MN∥AC
又由MN?平面ABC,AC?平面ABC
∴①直线MN∥平面ABC正确;
由于∠ACD=60°
∴AC与CD不垂直,则NM与CD也不垂直
故直线CD与平面BMN也不垂直
∴②直线CD⊥平面BMN错误;
∵三棱锥B-AMN与三棱锥B-ACM的高相等.
△AMN与△ACM高相等且底边之比为1:2
∴③三棱锥B-AMN的体积是三棱锥B-ACM的体积的一半正确.
故答案为:①、③
∴MN∥AC
又由MN?平面ABC,AC?平面ABC
∴①直线MN∥平面ABC正确;
由于∠ACD=60°
∴AC与CD不垂直,则NM与CD也不垂直
故直线CD与平面BMN也不垂直
∴②直线CD⊥平面BMN错误;
∵三棱锥B-AMN与三棱锥B-ACM的高相等.
△AMN与△ACM高相等且底边之比为1:2
∴③三棱锥B-AMN的体积是三棱锥B-ACM的体积的一半正确.
故答案为:①、③
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的性质及棱锥的体积,熟练掌握正四面体的几何特征,是解答本题的关键.

练习册系列答案
相关题目
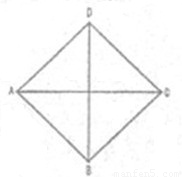
 我们将底面是正方形,侧棱长都相等的棱锥称为正四棱锥.已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同,且如图所示,视图中四边形ABCD是边长为1的正方形,则该几何体的体积为( )
我们将底面是正方形,侧棱长都相等的棱锥称为正四棱锥.已知由两个完全相同的正四棱锥组合而成的空间几何体的正视图、侧视图、俯视图都相同,且如图所示,视图中四边形ABCD是边长为1的正方形,则该几何体的体积为( )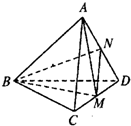 棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,
棱长都相等的四面体称为正四面体.在正四面体A-BCD中,点M,N分别是CD和AD的中点,