题目内容
13．若函数f（x）的零点为x=2，则函数y=f（2x-1）的零点为$\frac{3}{2}$．分析 只需令2x-1=2，就可以求出函数数y=f（2x-1）的零点$\frac{3}{2}$．
解答 解：因为函数f（x）的零点为x=2，即f（2）=0，
要求函数y=f（2x-1）的零点，
只需令2x-1=2，
解得x=$\frac{3}{2}$，即函数y=f（2x-1）的零点为为：x=$\frac{3}{2}$，
故答案为：$\frac{3}{2}$．
点评 本题主要考查了函数零点的定义和复合函数的零点的求法，属于基础题．
练习册系列答案
相关题目
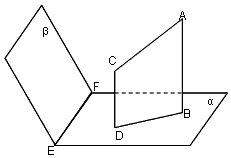假设平面α∩平面β=EF，AB⊥α，CD⊥β，垂足分别为B，D，若增加一个条件，就能推出BD⊥EF．现有下面四个条件：