题目内容
1.两互相平行的直线分别经过A(2,3),B(-1,-1),并且各自绕A,B旋转,则两平行直线的距离d的取值范围是(0,5].分析 设l1,l2之间的距离为d,依题意,可知0<d≤|AB|,从而可求得答案.
解答 解:设l1,l2之间的距离为d,
若直线l1,l2均经过点A(2,3),B(-1,-1),时,d=0,此时两直线变为一条直线,与题意不符,故d≠0,
∴d>0;
当直线AB与两平行直线l1,l2均垂直时,d最大,此时d=|AB|=$\sqrt{(2+1)^{2}+(3+1)^{2}}$=5,
∴l1,l2之间的距离的取值范围是(0,5].
故答案为:(0,5].
点评 本题考查两条平行直线间的距离,考查分析与空间想象及运算能力,属于中档题.

练习册系列答案
相关题目
10.等比数列{an}中,a1=3,a4=24,设数列{$\frac{1}{{a}_{n}}$}的前n项和为Sn,则S8等于( )
| A. | $\frac{85}{128}$ | B. | $\frac{21}{64}$ | C. | $\frac{63}{128}$ | D. | $\frac{35}{64}$ |
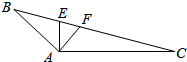 如图,在△ABC中,BC=3.AC=$\frac{3}{2}$$\sqrt{2}$,B=$\frac{π}{6}$,∠BAC$>\frac{π}{2}$,AE,AF是∠BAC的三等分角平分线,分别交BC于点E,F.
如图,在△ABC中,BC=3.AC=$\frac{3}{2}$$\sqrt{2}$,B=$\frac{π}{6}$,∠BAC$>\frac{π}{2}$,AE,AF是∠BAC的三等分角平分线,分别交BC于点E,F.