题目内容
已知数列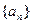 中,
中,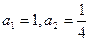 ,且
,且
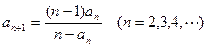 .
.
(1)求数列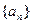 的通项公式;
的通项公式;
(2)求证:对一切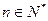 ,有
,有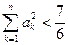 .
.
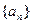 中,
中,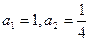 ,且
,且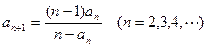 .
.(1)求数列
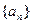 的通项公式;
的通项公式;(2)求证:对一切
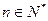 ,有
,有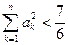 .
.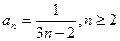
解(1)由已知,对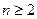 有
有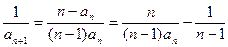 ,
,
两边同除以n,得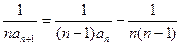 ,
,
即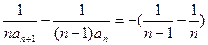 , ……………………5分
, ……………………5分
于是,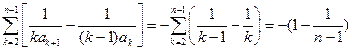 ,
,
即 ,
,
所以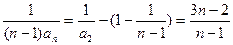 ,
,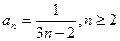 .
.
又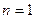 时也成立,故
时也成立,故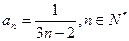 . ……………………10分
. ……………………10分
(2)当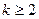 ,有
,有
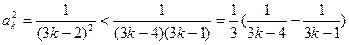 ,………………15分
,………………15分
所以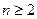 时,有
时,有
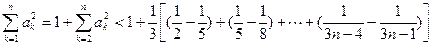
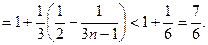
又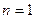 时,
时,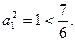
故对一切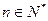 ,有
,有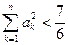 . ……………………20分
. ……………………20分
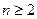 有
有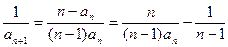 ,
,两边同除以n,得
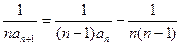 ,
,即
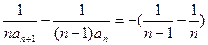 , ……………………5分
, ……………………5分于是,
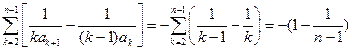 ,
, 即
 ,
,所以
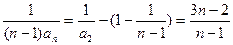 ,
,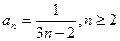 .
.又
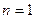 时也成立,故
时也成立,故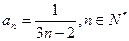 . ……………………10分
. ……………………10分(2)当
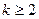 ,有
,有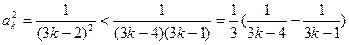 ,………………15分
,………………15分所以
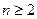 时,有
时,有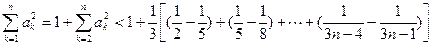
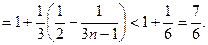
又
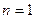 时,
时,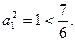
故对一切
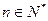 ,有
,有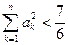 . ……………………20分
. ……………………20分
练习册系列答案
相关题目
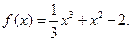

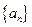 是正数组成的数列,前
是正数组成的数列,前 项和为
项和为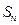 ,其中
,其中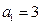 ,若点
,若点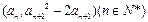
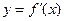 的图象上,求证:点
的图象上,求证:点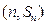 也在
也在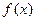 在区间
在区间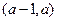 内的极值.
内的极值.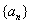 ,规定数列
,规定数列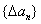 为数列
为数列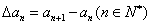 ;一般地,规定
;一般地,规定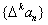 为
为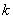 阶差分数列,其中
阶差分数列,其中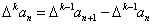 ,且
,且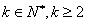 .
.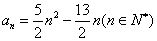 ,试证明
,试证明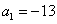 ,且满足
,且满足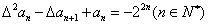 ,求数列
,求数列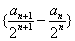 及
及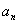 是否存在最小值,若存在求出其最小值,若不存在说明理由.
是否存在最小值,若存在求出其最小值,若不存在说明理由. 是首项为1公差为正的等差数列,数列
是首项为1公差为正的等差数列,数列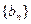 是首项为1的等比数列,设
是首项为1的等比数列,设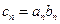
 ,且数列
,且数列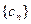 的前三项依次为1,4,12,
的前三项依次为1,4,12,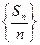 的前
的前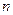 项的和Tn.
项的和Tn.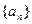 满足
满足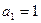 ,且对任意的
,且对任意的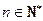 ,点
,点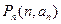 都有
都有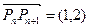 ,则数列
,则数列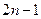
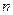
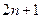
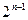
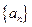 的前
的前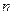 项和为
项和为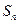 ,已知
,已知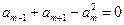
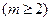 ,
,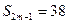 ,则
,则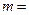 ( )
( )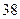
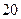
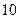
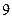
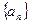 满足
满足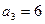 ,
,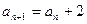 ,
,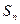 为其前
为其前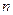 项和,则
项和,则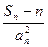 =___
=___ ______.
______.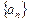 是等差数列,满足
是等差数列,满足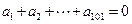 ,则有 ( )
,则有 ( )



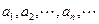 中的每一项都不为0。
中的每一项都不为0。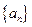 为等差数列的充分必要条件是:对任何
为等差数列的充分必要条件是:对任何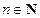 ,都有
,都有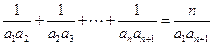 。
。