题目内容
(2008•徐汇区二模)已知关于x的方程x2-ax+ab=0,其中a,b为实数,且a≠0.
(1)若x=1-
i (i为虚数单位)是该方程的一个根,求a,b的值;
(2)当该方程没有实数根时,证明:
>
.
(1)若x=1-
| 3 |
(2)当该方程没有实数根时,证明:
| b |
| a |
| 1 |
| 4 |
分析:(1)由已知,得另一根为x′=1+
i,利用一元二次方程根与系数的关系求出a和b的值
(2)方程没有实数根,则△<0,化简后再证明.
| 3 |
(2)方程没有实数根,则△<0,化简后再证明.
解答:解:(1)根据一元二次方程有虚数解时,两根互为共轭虚数.由x=1-
i,得另一根为x′=1+
i,
由韦达定理得x+x′=a=2,ab=x•x′=(1-
i)(1+
i)=4,b=2.----------------(6分)
(2)方程没有实数根 则由△=a2-4ab<0⇒1-
<0⇒
>
----------(12分)
| 3 |
| 3 |
由韦达定理得x+x′=a=2,ab=x•x′=(1-
| 3 |
| 3 |
(2)方程没有实数根 则由△=a2-4ab<0⇒1-
| 4b |
| a |
| b |
| a |
| 1 |
| 4 |
点评:本题考查一元二次方程解,及根与系数的关系.若一元二次方程有虚数解,则两根互为共轭虚数,且韦达定理仍然成立.

练习册系列答案
相关题目
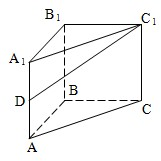 (2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点
(2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点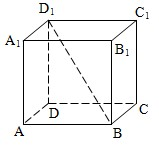 (2008•徐汇区二模)正方体ABCD-A1B1C1D1中,异面直线BD1与AA1所成的角的大小是
(2008•徐汇区二模)正方体ABCD-A1B1C1D1中,异面直线BD1与AA1所成的角的大小是